题目内容
（1）判断函数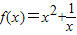
在（1，+∞）上的单调性，并用定义法加以证明；（2）若函数
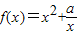在区间（1，+∞）上的单调递增，求实数a的取值范围．
【答案】分析：（1）利用函数单调性的定义进行证明．注意化简f（x2）-f（x1）是一定要化到最简．
（2）已知f（x）在区间（1，+∞）上单调递增，即f′（x）≥0在区间（1，+∞）上恒成立，然后用分离参数求最值即可．
解答：解：（1）f（x）在（1，+∞）上的单调递增 …（2分）
x1，x2是区间（1，+∞）上的任意两个值，且x1＜x2…（3分）
则x2-x1＞0，x1+x2＞2，x1x2＞1，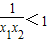
∴
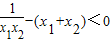…（5分）
=
=
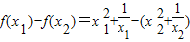
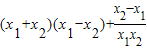
…（7分）
∴f（x1）＜f（x2）∴f（x）在（1，+∞）上的单调递增 …（8分）
（2）
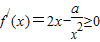在区间（1，+∞）上恒成立，∴a≤2x3在区间（1，+∞）上恒成立，∴a≤2．…（16分）
点评：本题考查函数单调性的判断和已知函数单调性求参数的范围，此类问题一般用导数解决，综合性较强．
（2）已知f（x）在区间（1，+∞）上单调递增，即f′（x）≥0在区间（1，+∞）上恒成立，然后用分离参数求最值即可．
解答：解：（1）f（x）在（1，+∞）上的单调递增 …（2分）
x1，x2是区间（1，+∞）上的任意两个值，且x1＜x2…（3分）
则x2-x1＞0，x1+x2＞2，x1x2＞1，
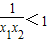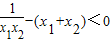∴…（5分）=
=
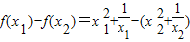
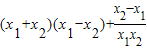
…（7分）∴f（x1）＜f（x2）∴f（x）在（1，+∞）上的单调递增 …（8分）
（2）
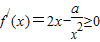在区间（1，+∞）上恒成立，∴a≤2x3在区间（1，+∞）上恒成立，∴a≤2．…（16分）点评：本题考查函数单调性的判断和已知函数单调性求参数的范围，此类问题一般用导数解决，综合性较强．
练习册系列答案
阅读快车系列答案
相关题目
是定义在[-1,1]上的奇函数，且
，若任意的
，当
时，总有
．
；
对所有的
恒成立，其中
（
是常数），求实数
的取值范围．
上的函数
，如果满足：对任意
，存在常数
，都有
成立，则称
称为函数
是否是有界函数，请写出详细判断过程；
，若
在
为上界，
在
为上界；
在
上是以3为上界的有界函数，
的取值范围.
上的函数
，如果满足：对任意
，存在常数
，都有
成立，则称
是
称为函数
是否是有界函数，请写出详细判断过程；
，若
在
为上界，
在
为上界；
在
上是以3为上界的有界函数，
的取值范围.