题目内容
高为8的圆台内有一个半径为2 的球O1,球心O1在圆台的轴上,球O1与圆台的上底面、侧面都相切,圆台内可再放入一个半径为3的球O2,使得球O2与球O1、圆台的下底面及侧面都只有一个公共点,除球O2,圆台内最多还能放入半径为3的球的个数是( )A.1
B.2
C.3
D.4
【答案】分析:根据放球的要求,加入的小球和球O2与球O1、圆台的下底面及侧面都只有一个公共点,即加入小球的球心与O2均匀分布在与底面距离为3,以到圆台的轴的距离为|OO2|=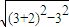 =4的圆周上.
=4的圆周上.
解答: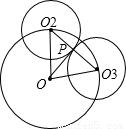 解:由分析可知:原问题即需要考查半径为4的圆周上均匀分布着几个半径为3且不相交的圆,如图所示,设∠POO2=∠POO3=α,
解:由分析可知:原问题即需要考查半径为4的圆周上均匀分布着几个半径为3且不相交的圆,如图所示,设∠POO2=∠POO3=α,
则sinα= ,∵
,∵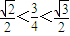 ,
,
∴45°<α<60°,
∴90°<2α<120°.故圆台内最多还能放入半径为3的球的个数是2.
故选B.
点评:本题需要较强的空间想象能力和计算能力,把问题进行恰当的转化是解决的关键.
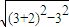 =4的圆周上.
=4的圆周上.解答:
 解:由分析可知:原问题即需要考查半径为4的圆周上均匀分布着几个半径为3且不相交的圆,如图所示,设∠POO2=∠POO3=α,
解:由分析可知:原问题即需要考查半径为4的圆周上均匀分布着几个半径为3且不相交的圆,如图所示,设∠POO2=∠POO3=α,则sinα=
 ,∵
,∵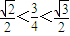 ,
,∴45°<α<60°,
∴90°<2α<120°.故圆台内最多还能放入半径为3的球的个数是2.
故选B.
点评:本题需要较强的空间想象能力和计算能力,把问题进行恰当的转化是解决的关键.

练习册系列答案
相关题目