题目内容
（中数量积）已知平面向量a=（x1，y1），b=（x2，y2），若|a|=2，|b|=3，a•b=-6，则
的值为（ ）A．-2
B．2
C．
D．
【答案】分析：先根据向量的数量积运算求出两向量夹角的余弦值，得到两向量的关系，然后用向量b表示出向量a，进而得到它们坐标之间的关系，最后可确定答案．
解答：解：设a，b的夹角为θ，则a•b=|a||b|cosθ=-6⇒cosθ=-1，
∴θ=180°．
即a，b共线且反向，
∴
，
，
∴
．
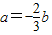故选C．
点评：本题主要考查向量的数量积运算．属基础题．
解答：解：设a，b的夹角为θ，则a•b=|a||b|cosθ=-6⇒cosθ=-1，
∴θ=180°．
即a，b共线且反向，
∴
，，∴
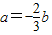．故选C．
点评：本题主要考查向量的数量积运算．属基础题．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
的值为（ ）
的值为（ ）
的值为（ ）
