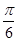题目内容
在 中,已知
中,已知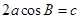 ,
,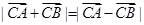 ,则
,则 为()
为()
| A.等边三角形 | B.等腰直角三角形 |
| C.锐角非等边三角形 | D.钝角三角形 |
B
解析试题分析:由余弦定理可知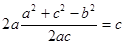 ,可得
,可得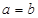 ,将
,将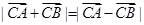 两边平方整理可得
两边平方整理可得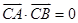 ,所以
,所以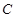 为直角,则
为直角,则 为等腰直角三角形.另:由正弦定理从角度也可推出
为等腰直角三角形.另:由正弦定理从角度也可推出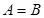 ,后者由向量的几何意义也可快速得出
,后者由向量的几何意义也可快速得出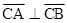 .
.
考点:余弦定理,向量的数量积运算.

练习册系列答案
相关题目
在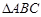 中,三边长
中,三边长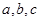 满足
满足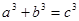 ,那么
,那么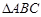 的形状为 ( )
的形状为 ( )
| A.锐角三角形 | B.钝角三角形 |
| C.直角三角形 | D.以上均有可能 |
若某人在点A测得金字塔顶端仰角为30°,此人往金字塔方向走了80米到达点B,测得金字塔顶端的仰角为45°,则金字塔的高度最接近于(忽略人的身高)(参考数据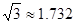 )
)
| A.110米 | B.112米 | C.220米 | D.224米 |
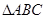 中,角
中,角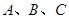 所对的边分别是
所对的边分别是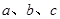 ,若角
,若角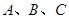 依次成等差数列,且
依次成等差数列,且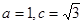 则
则 等于( ).
等于( ).
A.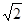 | B.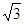 | C. | D.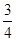 |
△ABC中,若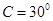 ,
,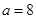 ,
,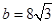 ,则
,则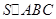 等于( )
等于( )
A.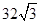 | B. | C.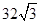 或 或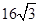 | D.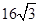 |
在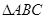 中,角A,B,C所对边分别为a,b,c,且
中,角A,B,C所对边分别为a,b,c,且 ,面积
,面积 ,则
,则 等于( )
等于( )
A. | B.5 | C. | D.25 |
若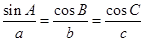 ,则
,则 是 ( )
是 ( )
| A.等边三角形 | B.有一内角是 的三角形 的三角形 |
| C.等腰直角三角形 | D.有一内角是 的等腰三角形 的等腰三角形 |
某人在C点测得某塔在南偏西80°,塔顶仰角为45°,此人沿南偏东40°方向前进10米到D,测得塔顶A的仰角为30°,则塔高为( )
| A.15米 | B.5米 |
| C.10米 | D.12米 |
 ABC中,角A、B、C的对边分别为a、b、c,若
ABC中,角A、B、C的对边分别为a、b、c,若 ,则角A等于
,则角A等于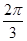 B.
B. C.
C.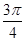 D.
D.