题目内容
已知sin +cos
+cos =
= ,
, ∈(0,
∈(0, ).求值:
).求值:
(1)tan ;(2)sin
;(2)sin -cos
-cos ;(3)sin3
;(3)sin3 +cos3
+cos3 .
.
 +cos
+cos =
= ,
, ∈(0,
∈(0, ).求值:
).求值:(1)tan
 ;(2)sin
;(2)sin -cos
-cos ;(3)sin3
;(3)sin3 +cos3
+cos3 .
.(1)tan =-
=- .(2)sin
.(2)sin -cos
-cos =
= .(3)sin3
.(3)sin3 +cos3
+cos3 =
=
 =-
=- .(2)sin
.(2)sin -cos
-cos =
= .(3)sin3
.(3)sin3 +cos3
+cos3 =
=
方法一 ∵sin +cos
+cos =
= ,
, ∈(0,
∈(0, ),
),
∴(sin +cos
+cos )2=
)2= =1+2sin
=1+2sin cos
cos ,
,
∴sin cos
cos =-
=- <0.
<0.
由根与系数的关系知,
sin ,cos
,cos 是方程x2-
是方程x2- x-
x- =0的两根,
=0的两根,
解方程得x1=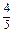 ,x2=-
,x2=- .
.
∵sin >0,cos
>0,cos >0,∴sin
>0,∴sin =
=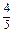 ,cosθ=-
,cosθ=- .
.
∴(1)tan =-
=- .(2)sin
.(2)sin -cos
-cos =
= .(3)sin3
.(3)sin3 +cos3
+cos3 =
= .
.
方法二 (1)同方法一.
(2)(sin -cos
-cos )2=1-2sin
)2=1-2sin ·cos
·cos
=1-2× =
= .
.
∵sin >0,cos
>0,cos <0,∴sin
<0,∴sin -cos
-cos >0,
>0,
∴sin -cos
-cos =
= .
.
(3)sin3 +cos3
+cos3 =(sin
=(sin +cos
+cos )(sin2
)(sin2 -sin
-sin cos
cos +cos2
+cos2 )
)
= ×
× =
= .
.
 +cos
+cos =
= ,
, ∈(0,
∈(0, ),
),∴(sin
 +cos
+cos )2=
)2= =1+2sin
=1+2sin cos
cos ,
,∴sin
 cos
cos =-
=- <0.
<0.由根与系数的关系知,
sin
 ,cos
,cos 是方程x2-
是方程x2- x-
x- =0的两根,
=0的两根,解方程得x1=
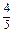 ,x2=-
,x2=- .
.∵sin
 >0,cos
>0,cos >0,∴sin
>0,∴sin =
=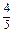 ,cosθ=-
,cosθ=- .
.∴(1)tan
 =-
=- .(2)sin
.(2)sin -cos
-cos =
= .(3)sin3
.(3)sin3 +cos3
+cos3 =
= .
.方法二 (1)同方法一.
(2)(sin
 -cos
-cos )2=1-2sin
)2=1-2sin ·cos
·cos
=1-2×
 =
= .
.∵sin
 >0,cos
>0,cos <0,∴sin
<0,∴sin -cos
-cos >0,
>0,∴sin
 -cos
-cos =
= .
.(3)sin3
 +cos3
+cos3 =(sin
=(sin +cos
+cos )(sin2
)(sin2 -sin
-sin cos
cos +cos2
+cos2 )
)=
 ×
× =
= .
.
练习册系列答案
相关题目
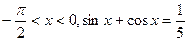 .
. 的值; (Ⅱ)求
的值; (Ⅱ)求 的值.
的值.  的终边在y轴上,求sin
的终边在y轴上,求sin ,且
,且 .
. 、
、 的值;
的值; 、
、 、
、 的值.
的值. ,则
,则 等于( )
等于( )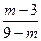



 ,
, ,则tan(p-q)的值为( )
,则tan(p-q)的值为( )



 =
= ,则sin2α= .
,则sin2α= .