题目内容
设 ,
, ,
,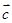 是空间任意的非零向量,且相互不共线,则以下命题中:
是空间任意的非零向量,且相互不共线,则以下命题中:
①( ·
· )·
)·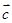 -(
-(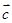 ·
· )·
)· =0;②
=0;②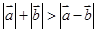 ;③若存在唯一实数组
;③若存在唯一实数组 使
使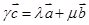 ,则
,则 ,
, ,
,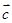 共面;④
共面;④ .
.
真命题的个数是( )
A. 0 B. 1 C. 2 D. 3
【答案】
B
【解析】
试题分析:对于①,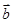 ,
, 是不共线的两个非零向量,又
是不共线的两个非零向量,又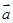 ·
·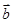 与
与 ·
·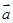 均不为零,所以①假命题;对于②,因为三角形两边之和大于第三边,所以②是真命题;对于③,当实数组
均不为零,所以①假命题;对于②,因为三角形两边之和大于第三边,所以②是真命题;对于③,当实数组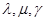 全为零时,则
全为零时,则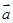 ,
,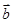 ,
, 可能不共面,所以③是假命题;对于④是假命题.故选B.
可能不共面,所以③是假命题;对于④是假命题.故选B.
考点:1.向量共线的基本定理;2.数乘向量的运算;3.向量数量积的几何意义.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
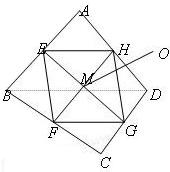 已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.
已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点. 为空间内任一非零向量,则适合条件
为空间内任一非零向量,则适合条件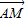 •
• =0的点M的轨迹是 .
=0的点M的轨迹是 .