题目内容
已知|a+b|<-c(a、b、c∈R),给出下列不等式:①a<-b-c;
②a>-b+c;
③a<b-c;
④|a|<|b|-c;
⑤|a|<-|b|-c.
其中一定成立的不等式是 (把成立的不等式的序号都填上)
【答案】分析:先根据绝对值不等式的性质可得到c<a+b<-c,进而可得到-b+c<a<-b-c,即可验证①②成立,③不成立,再结合|a+b|<-c,与|a+b|≥|a|-|b|,可得到|a|-|b|<-c即|a|<|b|-c成立,进而可验证④成立,⑤不成立,从而可确定答案.
解答:解:∵|a+b|<-c,∴c<a+b<-c.∴-b+c<a<-b-c.故①②成立,③不成立.
∵|a+b|<-c,|a+b|≥|a|-|b|,∴|a|-|b|<-c.∴|a|<|b|-c.
故④成立,⑤不成立.
故答案为:①②④
点评:本题主要考查不等式的基本性质.考查基础知识的综合运用.
解答:解:∵|a+b|<-c,∴c<a+b<-c.∴-b+c<a<-b-c.故①②成立,③不成立.
∵|a+b|<-c,|a+b|≥|a|-|b|,∴|a|-|b|<-c.∴|a|<|b|-c.
故④成立,⑤不成立.
故答案为:①②④
点评:本题主要考查不等式的基本性质.考查基础知识的综合运用.

练习册系列答案
相关题目

 ,b=sin
,b=sin ,则a, b,c的大小关系为
,则a, b,c的大小关系为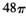 的球面上三点,且AB=2,BC=4,
的球面上三点,且AB=2,BC=4,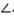 ABC=
ABC=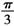 为球心,则二面角0-AB-C的大小为( )
为球心,则二面角0-AB-C的大小为( )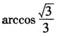 B.
B.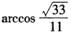 C.
C.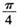 D.
D.