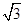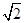题目内容
已知a,b,c均为正数,证明: 并确定a、b、
并确定a、b、
c为何值时,等号成立.
 并确定a、b、
并确定a、b、c为何值时,等号成立.
利用重要不等式a2+b2≥2ab来分析并证明,先展开,然后借助于不等式来得到。
试题分析:、证明 因为a,b,c均为正数,由均值不等式得
a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ac,
所以a2+b2+c2≥ab+bc+ac,①
同理
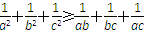 ,②
,②故
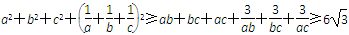 .③
.③所以原不等式成立.
当且仅当a=b=c时,①式和②式等号成立;
当且仅当a=b=c,(ab)2=(bc)2=(ac)2=3时,③式等号成立.
即当且仅当a=b=c=
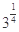 时,原式等号成立.
时,原式等号成立.点评:主要是考查了运用重要不等式进行放缩来证明不等式的方法,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
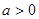 ,
,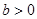 ,
, 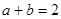 ,则
,则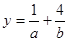 的最小值为 .
的最小值为 .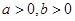 ,
,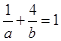 ,则
,则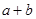 的最小值是 .
的最小值是 .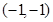 在直线
在直线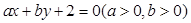 上,则
上,则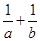 的最小值为( )
的最小值为( )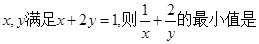 ( )
( )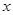 、
、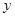 为正整数,且满足
为正整数,且满足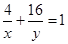 ,则
,则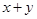 的最小值为_________;
的最小值为_________;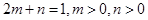 ,则
,则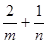 的最小值为 .
的最小值为 .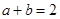 ,则
,则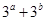 的最小值是 ( )
的最小值是 ( )