题目内容
若椭圆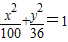 上一点P到其焦点F1的距离为6,则P到另一焦点F2的距离为 .
上一点P到其焦点F1的距离为6,则P到另一焦点F2的距离为 .
【答案】分析:根据椭圆的定义可得|PF1|+|PF2|=2a=20,结合P到其焦点F1的距离为6,可求P到另一焦点F2的距离.
解答:解:根据椭圆的定义可得|PF1|+|PF2|=2a=20
∵P到其焦点F1的距离为6,
∴|PF2|=20-6=14
即P到另一焦点F2的距离为14
故答案为:14.
点评:本题考查椭圆的定义,考查学生的计算能力,属于基础题.
解答:解:根据椭圆的定义可得|PF1|+|PF2|=2a=20
∵P到其焦点F1的距离为6,
∴|PF2|=20-6=14
即P到另一焦点F2的距离为14
故答案为:14.
点评:本题考查椭圆的定义,考查学生的计算能力,属于基础题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
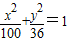 上一点P到其焦点F1的距离为6,则P到另一焦点F2的距离为 .
上一点P到其焦点F1的距离为6,则P到另一焦点F2的距离为 .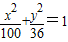 上一点P到其焦点F1的距离为6,则P到另一焦点F2的距离为 .
上一点P到其焦点F1的距离为6,则P到另一焦点F2的距离为 .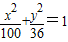 上一点P到其焦点F1的距离为6,则P到另一焦点F2的距离为 .
上一点P到其焦点F1的距离为6,则P到另一焦点F2的距离为 . 上一点P到其焦点F1的距离为6,则P到另一焦点F2的距离为 .
上一点P到其焦点F1的距离为6,则P到另一焦点F2的距离为 .