题目内容
设复数z满足条件|z|=1,那么 取最大值时的复数z为 .
取最大值时的复数z为 .
【答案】分析:复数的模转化为距离,|z|=1是单位圆上的点,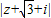 是单位圆上点与
是单位圆上点与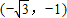 的距离的最大值,
的距离的最大值,
可求解答案.
解答:解:复数z满足条件|z|=1,它是复平面上的单位圆,那么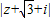 表示单位圆上的点到
表示单位圆上的点到 的距离,
的距离,
要使此距离取最大值的复数z,就是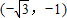 和)(0,0)连线和单位圆在第一象限的交点.
和)(0,0)连线和单位圆在第一象限的交点.
∵点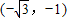 到原点距离是2.单位圆半径是1,此连线与单位圆在第一象限交点是
到原点距离是2.单位圆半径是1,此连线与单位圆在第一象限交点是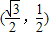 .
.
故答案为: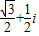
点评:本题考查复数的模的几何意义,复数和复平面内的点的一一对应,三角形相似,数形结合的思想,难度较大.
本题也可利用三角代换、复数辐角主值求解.
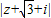 是单位圆上点与
是单位圆上点与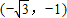 的距离的最大值,
的距离的最大值,可求解答案.
解答:解:复数z满足条件|z|=1,它是复平面上的单位圆,那么
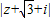 表示单位圆上的点到
表示单位圆上的点到 的距离,
的距离,要使此距离取最大值的复数z,就是
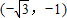 和)(0,0)连线和单位圆在第一象限的交点.
和)(0,0)连线和单位圆在第一象限的交点.∵点
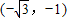 到原点距离是2.单位圆半径是1,此连线与单位圆在第一象限交点是
到原点距离是2.单位圆半径是1,此连线与单位圆在第一象限交点是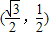 .
.故答案为:
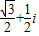
点评:本题考查复数的模的几何意义,复数和复平面内的点的一一对应,三角形相似,数形结合的思想,难度较大.
本题也可利用三角代换、复数辐角主值求解.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 的最大值是 .
的最大值是 .