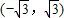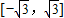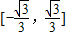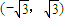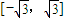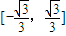Question

若过点A（3，0）的直线l与曲线（x-1）²+y²=1有公共点，则直线l斜率的取值范围为（　　）

• A、(-

  3

  ，

  3

  )
• B、[-

  3

  ，

  3

  ]
• C、(-

  3

  3

  ，

  3

  3

  )
• D、[-

  3

  3

  ，

  3

  3

  ]

Answer 1

分析：先设出直线的方程，代入圆的方程，利用判别式大于或等于0求得k的范围．

解答：解：设直线L的方程为y=k（x-3），
代入圆的方程中，整理得（k²+1）x²-（6k²+2）x+9k²=0
△=4（1-3k²）≥0．
解得-

3

3

≤k≤

3

3

故选D．

点评：本题主要考查了直线与圆锥曲线的关系．解题的步骤是一般是把直线与圆锥曲线的方程联立，利用判别式来判断直线与圆锥曲线的交点，或逆向使用．