题目内容
第一行是等差数列0,1,2,3,…,2006,将其相邻两项的和依次写下作为第二行,第二行相邻两项的和依次写下作为第三行,依此类推,共写出2007行.

(1)求证:第1行至第2006行各行都构成等差数列.(定义只有两项的数列a1,a2也称等差数列);
(2)各行的公差组成数列{di}(i=1,2,3,…,2006).求通项公式di;
(3)各行的第一个数组成数列{aj}(j=1,2,3,…,2006),求通项公式aj;
(4)求2007行的这个数.
解:(1)记ai•j表示第i行第j列的项.由已知知第1行是等差数列;a2•(k+1)-a2•k=a1•(k+1)+a1•(k+2)-(a1•k+a1•(k+1))=a1•(k+2)-a1•k=2,
所以第2行数列是等差数列.a3•(k+1)-a3•k=a2•(k+1)+a2•(k+2)-(a2•k+a2•(k+1))=a2•(k+2)-a2•k=4,
所以第3行数列是等差数列.
同理可证,第4,5,…,都是等差数列.
(2)di+1=a(i+1)•(k+1)-a(i+1)•k=ai•(k+1)+ai•(k+2)-ai•k-ai•(k+1)=ai•(k+2)-ai•k=2di,
∴ ,则{di}是等差数列,di=d1•2i-1=2i-1.
,则{di}是等差数列,di=d1•2i-1=2i-1.
(3)aj+1=aj+aj•2=aj+aj+dj=2aj+2j-1,
∴ .
.
∴数列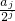 是等差数列,
是等差数列, ,
,
所以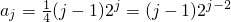 .
.
(4)由(3)aj=(j-1)•2j-2可知a2007=2006•22005.
分析:(1)记ai•j表示第i行第j列的项.由已知知第1行是等差数列;推出第2行满足a3•(k+1)-a3•k=4是等差数列,类比推出第1行至第2006行各行都构成等差数列;
(2)通过di+1=a(i+1)•(k+1)-a(i+1)•k=2di,即可求出通项公式di;
(3)利用aj+1=aj+aj•2=aj+aj+dj=2aj+2j-1,推出数列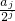 是等差数列,然后求通项公式aj;
是等差数列,然后求通项公式aj;
(4)利用(3)直接求2007行的这个数.
点评:本题是中档题,考查数列的有关知识,证明数列是等差数列,数列的递推关系式的应用,数列与函数的综合应用,考查计算能力.
所以第2行数列是等差数列.a3•(k+1)-a3•k=a2•(k+1)+a2•(k+2)-(a2•k+a2•(k+1))=a2•(k+2)-a2•k=4,
所以第3行数列是等差数列.
同理可证,第4,5,…,都是等差数列.
(2)di+1=a(i+1)•(k+1)-a(i+1)•k=ai•(k+1)+ai•(k+2)-ai•k-ai•(k+1)=ai•(k+2)-ai•k=2di,
∴
 ,则{di}是等差数列,di=d1•2i-1=2i-1.
,则{di}是等差数列,di=d1•2i-1=2i-1.(3)aj+1=aj+aj•2=aj+aj+dj=2aj+2j-1,
∴
 .
.∴数列
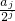 是等差数列,
是等差数列, ,
,所以
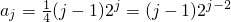 .
.(4)由(3)aj=(j-1)•2j-2可知a2007=2006•22005.
分析:(1)记ai•j表示第i行第j列的项.由已知知第1行是等差数列;推出第2行满足a3•(k+1)-a3•k=4是等差数列,类比推出第1行至第2006行各行都构成等差数列;
(2)通过di+1=a(i+1)•(k+1)-a(i+1)•k=2di,即可求出通项公式di;
(3)利用aj+1=aj+aj•2=aj+aj+dj=2aj+2j-1,推出数列
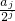 是等差数列,然后求通项公式aj;
是等差数列,然后求通项公式aj;(4)利用(3)直接求2007行的这个数.
点评:本题是中档题,考查数列的有关知识,证明数列是等差数列,数列的递推关系式的应用,数列与函数的综合应用,考查计算能力.

练习册系列答案
相关题目
