题目内容
等差数列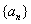 的前
的前 项和为
项和为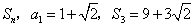 .
.
(1)求数列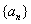 的通项
的通项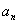 与前
与前 项和
项和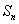 ;
;
(2)设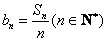 ,求证:数列
,求证:数列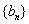 中任意不同的三项都不可能成为等比数列。
中任意不同的三项都不可能成为等比数列。
【答案】
解:(1)由已知得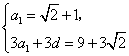 ,
,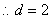 ,
,
故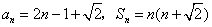 .
.
(2)由(Ⅰ)得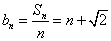 .
.
假设数列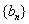 中存在三项
中存在三项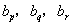 (
(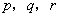 互不相等)成等比数列,则
互不相等)成等比数列,则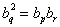 .
.
即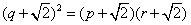 .
.
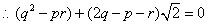
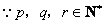 ,
,
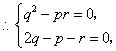
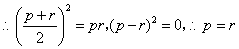 .
.
与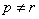 矛盾.
矛盾.
所以数列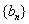 中任意不同的三项都不可能成等比数列。
中任意不同的三项都不可能成等比数列。
点评:本题证明推出的结果是与题设矛盾。?
本问题推出的结果是与题设不矛盾,可能是数列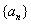 、数列
、数列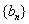 混淆了。
混淆了。

练习册系列答案
相关题目
 的前
的前 项和为
项和为 .若
.若 是
是 的等比中项,
的等比中项,  ,则
,则 等于()
等于() 的前
的前 项和为
项和为 ,若
,若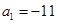 ,
, ,则当
,则当