题目内容
(1)已知二次函数f(x)满足:f(2)=-1,f(-1)=-1,且f(x)的最大值为8,求此二次函数的 解析式.(2)计算
 .
.
【答案】分析:(1)由于二次函数满足f(2)=f(-1),得到对称轴为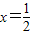 ,又知最大值,得到代入其中一点,进而得到函数的解析式;
,又知最大值,得到代入其中一点,进而得到函数的解析式;
(2)依据对数运算法则及换底公式,得到即可.
解答:解:(1)∵二次函数f(x)满足:f(2)=-1,f(-1)=-1,
∴此函数对称轴为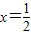 ,
,
又∵f(x)的最大值为8,
∴可设f(x)=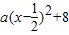 ,代入f(2)=-1,
,代入f(2)=-1,
∴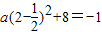 ,∴a=4,
,∴a=4,
所以函数f(x)=-4x2+4x+7;
(2)
=(1+lg2)×(1-lg2)+lg22-log232
=1-5=-4.
点评:本题考查了二次函数的解析式及对数的运算.注意:对任意实数t都有f (a+t)=f (b-t),得到对称轴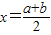 ;换底公式:
;换底公式: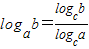 .
.
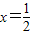 ,又知最大值,得到代入其中一点,进而得到函数的解析式;
,又知最大值,得到代入其中一点,进而得到函数的解析式;(2)依据对数运算法则及换底公式,得到即可.
解答:解:(1)∵二次函数f(x)满足:f(2)=-1,f(-1)=-1,
∴此函数对称轴为
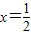 ,
,又∵f(x)的最大值为8,
∴可设f(x)=
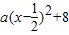 ,代入f(2)=-1,
,代入f(2)=-1,∴
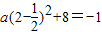 ,∴a=4,
,∴a=4,所以函数f(x)=-4x2+4x+7;
(2)

=(1+lg2)×(1-lg2)+lg22-log232
=1-5=-4.
点评:本题考查了二次函数的解析式及对数的运算.注意:对任意实数t都有f (a+t)=f (b-t),得到对称轴
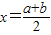 ;换底公式:
;换底公式: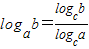 .
. 
练习册系列答案
相关题目
 ,求f(x)的解析式;
,求f(x)的解析式;