题目内容
设实数x,y满足不等式组
,若z=x+3y的最大值为12,则实数k的值为
|
-9
-9
.分析:先画出线性约束条件表示的可行域,再讨论k的正负,将目标函数看作是斜率为-
的动直线,数形结合找到最优解,代入目标函数即可的最大值,最后利用已知列方程解得k的值
| 1 |
| 3 |
解答:解:画出可行域如图: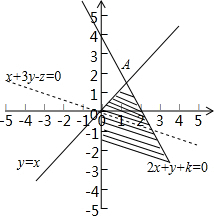 目标函数z=x+3y可看作是斜率为-
目标函数z=x+3y可看作是斜率为-
的动直线
若k≥0,则数形结合可知最优解为(0,-k),此时,z=0-3k<0,不可能为12,故k<0,
可行域为如图阴影部分,
由
得A(-
,-
)
数形结合可知点A为最优解,
∴z=-
+3×(-
)=-
=12
解得k=-9
故答案为-9
 目标函数z=x+3y可看作是斜率为-
目标函数z=x+3y可看作是斜率为-| 1 |
| 3 |
若k≥0,则数形结合可知最优解为(0,-k),此时,z=0-3k<0,不可能为12,故k<0,
可行域为如图阴影部分,
由
|
| k |
| 3 |
| k |
| 3 |
数形结合可知点A为最优解,
∴z=-
| k |
| 3 |
| k |
| 3 |
| 4k |
| 3 |
解得k=-9
故答案为-9
点评:本题主要考查了线性规划的解题思想和解题方法,线性约束条件及其可行域,分类讨论的思想方法,数形结合的思想方法

练习册系列答案
相关题目