题目内容
已知二次项系数为1的二次函数![]() ,当且仅当x∈(0,2)时f(x)<0,数列
,当且仅当x∈(0,2)时f(x)<0,数列![]() 的前n项和为
的前n项和为![]() ,点
,点![]() 均在函数
均在函数![]() 的图像上
的图像上![]()
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,
,![]() 是数列
是数列![]() 的前n项和,求使得
的前n项和,求使得![]() 对所有
对所有![]() 都成立的最大正整数m;
都成立的最大正整数m;
解:(Ⅰ)设这二次函数为f(x)=x2+bx+c , 由f(x)<0的解集为(0,2),得
b=-2, c=0,所以 f(x)=x2-2x![]()
又因为点![]() 均在函数
均在函数![]() 的图像上,所以
的图像上,所以![]() =n2-2n
=n2-2n![]()
当n≥2时,an=Sn-Sn-1=(n2-2n)-![]() =2n-3
=2n-3![]()
当n=1时,a1=S1=12-2=-1,所以,an=2n-3![]() (n∈N+)
(n∈N+)
(Ⅱ)由(Ⅰ)得,![]() =
=![]() =
=![]() ,
,
故Tn=![]() =-3+
=-3+![]()
![]() =-3+
=-3+![]() (1-
(1-![]() )
)![]()
![]()
因此,要使![]() (
(![]() )成立的m,必须且仅须满足
)成立的m,必须且仅须满足![]() ≤
≤![]() ,
,
即m≤30,所以满足要求的最大正整数m为30![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 对任意
对任意 ,都有
,都有 成立,设向量
成立,设向量 (sinx,2),
(sinx,2), (2sinx,
(2sinx, ),
), (cos2x,1),
(cos2x,1), (1,2),当
(1,2),当 时,不等式f(
时,不等式f( )>f(
)>f( )的解集为
)的解集为  对任意
对任意 ,都有
,都有 成立,设向量
成立,设向量 (sinx,2),
(sinx,2), (2sinx,
(2sinx, ),
), (cos2x,1),
(cos2x,1),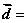 (1,2),当
(1,2),当 [0,
[0, ]时,不等式f(
]时,不等式f( )>f(
)>f( )的解集为
。
)的解集为
。