题目内容
设函数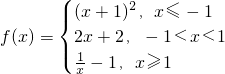 ,已知f(a)>1,则实数a的取值范围是________.
,已知f(a)>1,则实数a的取值范围是________.
{a|a<-2或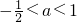 }
}
分析:通过分段函数,求出每一段不等式的解集,然后求出a的范围即可.
解答:因为函数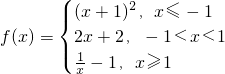 ,已知f(a)>1,
,已知f(a)>1,
所以当a≤-1时,(a+1)2>1,解得a<-2.
当-1<a<1时,2a+2>1,解得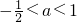 .
.
当a≥1时,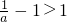 ,解得a∈∅.
,解得a∈∅.
综上a的范围是{a|a<-2或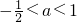 }.
}.
故答案为:{a|a<-2或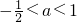 }.
}.
点评:本题考查分段函数与不等式的解法,考查分类讨论思想,计算能力.
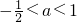 }
}分析:通过分段函数,求出每一段不等式的解集,然后求出a的范围即可.
解答:因为函数
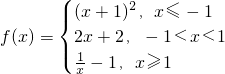 ,已知f(a)>1,
,已知f(a)>1,所以当a≤-1时,(a+1)2>1,解得a<-2.
当-1<a<1时,2a+2>1,解得
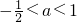 .
.当a≥1时,
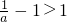 ,解得a∈∅.
,解得a∈∅.综上a的范围是{a|a<-2或
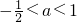 }.
}.故答案为:{a|a<-2或
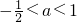 }.
}.点评:本题考查分段函数与不等式的解法,考查分类讨论思想,计算能力.

练习册系列答案
相关题目
 ,已知f(a)>1,则实数a的取值范围是( )
,已知f(a)>1,则实数a的取值范围是( ) ,已知f(a)>1,则a的取值范围为( )
,已知f(a)>1,则a的取值范围为( ) ,已知f(a)>1,则实数a的取值范围是( )
,已知f(a)>1,则实数a的取值范围是( ) ,已知f(a)>1,则实数a的取值范围是( )
,已知f(a)>1,则实数a的取值范围是( )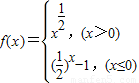 ,已知f(a)>1,则a的取值范围为( )
,已知f(a)>1,则a的取值范围为( )