题目内容
借助计算机(器)作某些分段函数图象时,分段函数的表示有时可以利用函数 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).设f(x)=(-x2+4x-3)S(x-1)+(x2-1)S(1-x).
(Ⅰ)请把函数f(x)写成分段函数的形式;
(Ⅱ)设F(x)=f(x-k),且F(x)为奇函数,写出满足条件的k值;(不需证明)
(Ⅲ)设h(x)=(x2-x+a-a2)S(x-a)+(x2+x-a-a2)S(a-x),求函数h(x)的最小值.
【答案】分析:(I)分当x>1、当x=1和当x<1时3种情况加以讨论,分别根据S(x)的对应法则代入,可得f(x)相应范围内的表达式,最后综合可得函数f(x)写成分段函数的形式;
(II)因为函数F(x)的定义域为R,所以F(x)为奇函数,得F(0)=f(-k)=0,由此结合-k的范围代入f(x)的表达式,再根据奇函数的定义加以验证,即可得到满足条件的k值;
(III)由题意,可得 ,再结合二次函数的图象与性质,分a≥
,再结合二次函数的图象与性质,分a≥ 、0≤a<
、0≤a< 、-
、- <a<0和a≤-
<a<0和a≤- 的4种情况进行讨论,最后综合可得当a≤0时,h(x)的最小值为
的4种情况进行讨论,最后综合可得当a≤0时,h(x)的最小值为 ;当a>0时,h(x)的最小值为
;当a>0时,h(x)的最小值为 .
.
解答:解:(Ⅰ)分情况讨论:
①当x>1时,S(x-1)=1且S(1-x)=0,得f(x)=(-x2+4x-3)×1+(x2-1)×0=-x2+4x-3;
②当x=1时,S(x-1)=S(1-x)=1,得f(x)=(-x2+4x-3)×1+(x2-1)×1=4x-4;
③当x<1时,S(x-1)=0且S(1-x)=1,得f(x)=(-x2+4x-3)×0+(x2-1)×1=x2-1
∴ …(2分)
…(2分)
(Ⅱ)若F(x)为奇函数,则F(0)=f(-k)=0,
①当-k>1时,解出k=-1或-3,但k=-3不符合题意;②当-k=1时,解出f(-k)=0,恒成立,得k=-1;
③当-k<1时,解出k=-1或1,但k=1不符合题意
综上所述,得当k=-1时,F(x)为奇函数.…(4分)
(Ⅲ)由已知,得
并且函数s=x2-x+a-a2与t=x2+x-a-a2在x=a处的值相同.…(5分)
①当 时,h(x)在区间
时,h(x)在区间 上单调递减,在区间
上单调递减,在区间 上单调递增,在区间(a,+∞)上单调递增.
上单调递增,在区间(a,+∞)上单调递增.
所以,h(x)的最小值为 .…(6分)
.…(6分)
当 时,h(x)在区间
时,h(x)在区间 上单调递减,在区间
上单调递减,在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,在区间
上单调递减,在区间 上单调递增.
上单调递增.
所以h(x)最小值为 与
与 中较小的一个,即
中较小的一个,即 与
与 中较小的一个.
中较小的一个.
②当 时,h(x)的最小值为
时,h(x)的最小值为 .…(7分)
.…(7分)
③当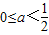 时,h(x)的最小值为
时,h(x)的最小值为 .…(8分)
.…(8分)
④当 时,在区间(-∞,a)上单调递减,在区间
时,在区间(-∞,a)上单调递减,在区间 上单调递减,在区间
上单调递减,在区间 上单调递增.
上单调递增.
所以h(x)的最小值为 .…(9分)
.…(9分)
综上所述,得:当a≤0时,h(x)的最小值为 ,当a>0时,h(x)的最小值为
,当a>0时,h(x)的最小值为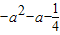 .…(10分)
.…(10分)
点评:本题以分段函数和含有字母参数的二次函数为载体,讨论函数的单调性、奇偶性与最小值,着重考查了基本初等函数的图象与性质、函数解析式的求解及常用方法和奇偶性与单调性的综合等知识,属于难题.
(II)因为函数F(x)的定义域为R,所以F(x)为奇函数,得F(0)=f(-k)=0,由此结合-k的范围代入f(x)的表达式,再根据奇函数的定义加以验证,即可得到满足条件的k值;
(III)由题意,可得
 ,再结合二次函数的图象与性质,分a≥
,再结合二次函数的图象与性质,分a≥ 、0≤a<
、0≤a< 、-
、- <a<0和a≤-
<a<0和a≤- 的4种情况进行讨论,最后综合可得当a≤0时,h(x)的最小值为
的4种情况进行讨论,最后综合可得当a≤0时,h(x)的最小值为 ;当a>0时,h(x)的最小值为
;当a>0时,h(x)的最小值为 .
.解答:解:(Ⅰ)分情况讨论:
①当x>1时,S(x-1)=1且S(1-x)=0,得f(x)=(-x2+4x-3)×1+(x2-1)×0=-x2+4x-3;
②当x=1时,S(x-1)=S(1-x)=1,得f(x)=(-x2+4x-3)×1+(x2-1)×1=4x-4;
③当x<1时,S(x-1)=0且S(1-x)=1,得f(x)=(-x2+4x-3)×0+(x2-1)×1=x2-1
∴
 …(2分)
…(2分)(Ⅱ)若F(x)为奇函数,则F(0)=f(-k)=0,
①当-k>1时,解出k=-1或-3,但k=-3不符合题意;②当-k=1时,解出f(-k)=0,恒成立,得k=-1;
③当-k<1时,解出k=-1或1,但k=1不符合题意
综上所述,得当k=-1时,F(x)为奇函数.…(4分)
(Ⅲ)由已知,得

并且函数s=x2-x+a-a2与t=x2+x-a-a2在x=a处的值相同.…(5分)
①当
 时,h(x)在区间
时,h(x)在区间 上单调递减,在区间
上单调递减,在区间 上单调递增,在区间(a,+∞)上单调递增.
上单调递增,在区间(a,+∞)上单调递增.所以,h(x)的最小值为
 .…(6分)
.…(6分)当
 时,h(x)在区间
时,h(x)在区间 上单调递减,在区间
上单调递减,在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,在区间
上单调递减,在区间 上单调递增.
上单调递增.所以h(x)最小值为
 与
与 中较小的一个,即
中较小的一个,即 与
与 中较小的一个.
中较小的一个.②当
 时,h(x)的最小值为
时,h(x)的最小值为 .…(7分)
.…(7分)③当
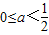 时,h(x)的最小值为
时,h(x)的最小值为 .…(8分)
.…(8分)④当
 时,在区间(-∞,a)上单调递减,在区间
时,在区间(-∞,a)上单调递减,在区间 上单调递减,在区间
上单调递减,在区间 上单调递增.
上单调递增.所以h(x)的最小值为
 .…(9分)
.…(9分)综上所述,得:当a≤0时,h(x)的最小值为
 ,当a>0时,h(x)的最小值为
,当a>0时,h(x)的最小值为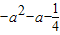 .…(10分)
.…(10分)点评:本题以分段函数和含有字母参数的二次函数为载体,讨论函数的单调性、奇偶性与最小值,着重考查了基本初等函数的图象与性质、函数解析式的求解及常用方法和奇偶性与单调性的综合等知识,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
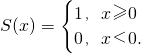 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x). 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).