题目内容

已知集合U = {(x，y)| xÎR, y ÎR}, M = {(x，y) | |x | + | y | < a }，P = {(x，y)| y = f (x ) }，现给出下列函数： ①y = ax , ② y = logax , ③y = sin(x + a), ④y = cos a x，若0 < a < 1时，恒有P∩CUM = P，则f (x)可以取的函数有

A.①②③        B. ①②④       C. ①③④    D . ②③④

 

【答案】

B

【解析】∵∁uM={（x，y）||x|+|y|≥a}，0＜a＜1时，P∩∁uM=P，∴P={（x，y）y=f（x）}⊆∁uM，如图所示：结合图形可得满足条件的函数图象应位于曲线|x|+|y|=a（-a≤x≤a ）的上方．

①中，x∈R，y＞0，满足|x|+|y|≥a，故①可取．

②中，x＞0，y=logax∈R，满足||x|+|y|≥a，故②可取．

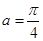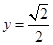③中的函数不满足条件，如  x=0，时，，不满足|x|+|y|≥a．

④中x∈R，-1≤y≤1，满足|x|+|y|≥a，故④可取．

 

练习册系列答案
相关题目
5、已知集合U={1，2，3，4，5}，A={2，3，4}，B={4，5}，则A∩（CUB）=
{2，3}
已知集合U={0，2，4，6，8，10}，A={2，4，6}，B={2}，则（?UA）∪B是（　　）
已知集合U=R，A={y|y=log2x，x＞1}，B={y|y=(
12
)x，x＞1}，求(CUA)∩B．
已知集合U={1，2，3，4}，A={2，4}，B={3，4}，则（?UA）∪B=（　　）
已知集合U={1，2，3，4，5，6}，A={1，3，4}，则?UA=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网