题目内容
一个水池容积为100m3,装有甲、乙、丙三个水管,甲乙为进水管,丙为出水管.单开甲管2小时可将空水池注满,单开乙管3小时可将空水池注满,单开丙管6小时将满池水放空.三管齐开,1.8小时后水池中的水量为
100
100
m3.分析:这也是一个工作效率的问题,由题可得三管的工作效率分别为:100×
、100×
、100×
,设三管一齐开放,x小时水池中水量为y,则可列式y=100(
+
-
)×x求解.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
解答:解:设三管齐放,x小时水池中水量为y,则有:
y=100(
+
-
)×x=100(
+
-
)×1.8=120>100
∴1.8小时后水池中的水量为 100m3.
故答案为:100.
y=100(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
∴1.8小时后水池中的水量为 100m3.
故答案为:100.
点评:本题主要考查了函数模型的选择与应用.找到合适的等量关系是解决问题的关键;难点是找到两种水管的工作效率,根据工作总量=工作时间×工作效率求解.

练习册系列答案
相关题目
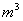 ,装有甲、乙、丙三个水管,甲乙为进水管,丙为出水管。单开甲管2小时可将空水池注满,单开乙管3小时可将空水池注满,单开丙管6小时将满池水放空。三管齐开,1.8小时后水池中的水量为 ▲
,装有甲、乙、丙三个水管,甲乙为进水管,丙为出水管。单开甲管2小时可将空水池注满,单开乙管3小时可将空水池注满,单开丙管6小时将满池水放空。三管齐开,1.8小时后水池中的水量为 ▲