题目内容
tan18°+tan42°+| 3 |
分析：观察发现：18°+42°=60°，故利用两角和的正切函数公式表示出tan（18°+42°），利用特殊角的三角函数值化简，变形后即可得到所求式子的值．
解答：解：由tan60°=tan（18°+42°）=
=
，
得到tan18°+tan42°=
（1-tan18°tan42°），
则tan18°+tan42°+
tan18°•tan42°=
．
故答案为：
．
| tan18°+tan42° |
| 1-tan18°tan42° |
| 3 |
得到tan18°+tan42°=
| 3 |
则tan18°+tan42°+
| 3 |
| 3 |
故答案为：
| 3 |
点评：此题考查了两角和与差得正切函数公式，以及特殊角的三角函数值．观察所求式子中的角度的和为45°，联想到利用45°角的正切函数公式是解本题的关键．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
相关题目
=________．
= ．
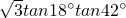