题目内容
 (2012•福建)如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.
(2012•福建)如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.(1)求三棱锥A-MCC1的体积;
(2)当A1M+MC取得最小值时,求证:B1M⊥平面MAC.
分析:(1)由题意可知,A到平面CDD1C1的距离等于AD=1,易求S△MCC1=1,从而可求VA-MCC1;
(2)将侧面CDD1C1绕DD1逆时针转90°展开,与侧面ADD1A1共面,当A1,M,C′共线时,A1M+MC取得最小值.易证CM⊥平面B1C1M,从而CM⊥B1M,同理可证,B1M⊥AM,
问题得到解决.
(2)将侧面CDD1C1绕DD1逆时针转90°展开,与侧面ADD1A1共面,当A1,M,C′共线时,A1M+MC取得最小值.易证CM⊥平面B1C1M,从而CM⊥B1M,同理可证,B1M⊥AM,
问题得到解决.
解答:解:(1)由长方体ABCD-A1B1C1D1知,AD⊥平面CDD1C1,
∴点A到平面CDD1C1的距离等于AD=1,
又S△MCC1=
CC1×CD=
×2×1=1,
∴VA-MCC1=
AD•S△MCC1=
.
(2)将侧面CDD1C1绕DD1逆时针转90°展开,与侧面ADD1A1共面,
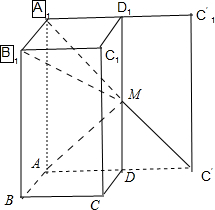
当A1,M,C′共线时,A1M+MC取得最小值.
由AD=CD=1,AA1=2,得M为DD1的中点.连接C1M,在△C1MC中,C1M=
,MC=
,C1C=2,
∴C1C2=C1M2+MC2,得∠CMC1=90°,即CM⊥C1M,又B1C1⊥平面CDD1C1,
∴B1C1⊥CM,又B1C1∩C1M=C1,
∴CM⊥平面B1C1M,
∴CM⊥B1M,同理可证,B1M⊥AM,又AM∩MC=M,
∴B1M⊥平面MAC
∴点A到平面CDD1C1的距离等于AD=1,
又S△MCC1=
| 1 |
| 2 |
| 1 |
| 2 |
∴VA-MCC1=
| 1 |
| 3 |
| 1 |
| 3 |
(2)将侧面CDD1C1绕DD1逆时针转90°展开,与侧面ADD1A1共面,

当A1,M,C′共线时,A1M+MC取得最小值.
由AD=CD=1,AA1=2,得M为DD1的中点.连接C1M,在△C1MC中,C1M=
| 2 |
| 2 |
∴C1C2=C1M2+MC2,得∠CMC1=90°,即CM⊥C1M,又B1C1⊥平面CDD1C1,
∴B1C1⊥CM,又B1C1∩C1M=C1,
∴CM⊥平面B1C1M,
∴CM⊥B1M,同理可证,B1M⊥AM,又AM∩MC=M,
∴B1M⊥平面MAC
点评:本题考查直线与直线、直线与平面的位置关系及几何体的体积等知识,考查空间想象能力、推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想,属于难题.

练习册系列答案
相关题目
 (2012•福建)如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2012•福建)如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )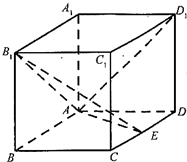 (2012•福建)如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.
(2012•福建)如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点. (2012•福建)如图,等边三角形OAB的边长为
(2012•福建)如图,等边三角形OAB的边长为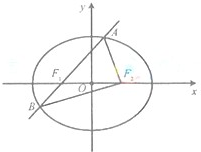 (2012•福建)如图,椭圆E:
(2012•福建)如图,椭圆E: