题目内容
已知函数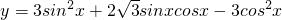
，（x∈R），
（1）写出这个函数的振幅，初相和最小正周期；
（2）求y的最大值及此时x的值；
（3）写出这个函数的单调增区间；
（4）画出这个函数的图象，并说出它是怎样由y=sinx的图象变换而得到的？
解：函数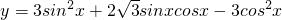
=
=
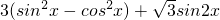
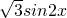-3cos2x
∴
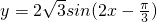
（1）
3’
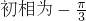4’最小正周期为π5’
（2）
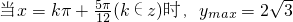7’
（3）
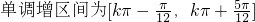8’
（4）
分析：利用二倍角及辅助角公式化简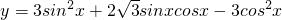可得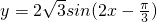，，根据三角函数的性质可分别求解
点评：本题主要考查看三角函数的性质的求解，解题的关键是利用二倍角及辅助角公式对函数化简为y=Asin（wx+∅）的形式，熟练掌握正弦函数的性质是解决本题的令一个关键．
=
=
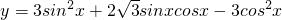
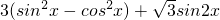
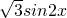-3cos2x∴
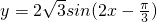
（1）
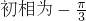3’4’最小正周期为π5’（2）
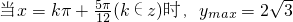7’（3）
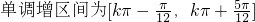8’（4）
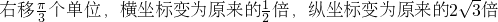
分析：利用二倍角及辅助角公式化简
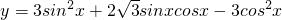可得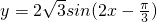，，根据三角函数的性质可分别求解点评：本题主要考查看三角函数的性质的求解，解题的关键是利用二倍角及辅助角公式对函数化简为y=Asin（wx+∅）的形式，熟练掌握正弦函数的性质是解决本题的令一个关键．
练习册系列答案
相关题目
（其中x∈R，A＞0，ω＞0）的图象与x轴的交点中，相邻两个交点之间的距离为
，且图象上一个点为
．
恒成立；q：函数y=（m2-1）x是增函数．若“p或q”为真，“p且q”为假，求实数m的取值范围．
（其中x∈R，A＞0，ω＞0）的最大值为2，最小正周期为8．
，其中x∈R，则下列结论中正确的是（ ）
的图象左移
得到函数f（x）的图象
（x∈R，且x≠1），那么它的反函数为（ ）
（x∈R，且x≠1）
（x∈R，且x≠6）
（x∈R，且x≠-
）
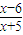（x∈R，且x≠-5）