题目内容
已知三边都不相等的三角形ABC的三内角A、B、C满足sinAcosB+sinB=sinAcosC+sinC,设复数z1=cosθ+isinθ(0<θ<π且θ≠| π |
| 2 |
| 2 |
. |
| z2 |
分析:将已知的等式变形化简,求出角A的大小,计算2个复数的积,并化为三角形式,由辐角求辐角主值,注意辐角主值的范围.
解答:解:∵sinAcosB+sinB=sinAcosC+sinC
∴sinA(cosB-cosC)=sinC-sinB
得4sin
cos
(-sin
×sin
)=-2sin
cos
(3分)
∵
=
-
,∴cos
=sin
,sin
=cos
,又
≠0,
∴sin
≠0,sin
≠0.上式化简为cos2
=
∴A=
(6分)
z1
=
[cos(θ-
)+isin(θ-
)](9分)
∴当0<θ<
时,arg(z1
)=
+θ
当
<θ<π时,arg(z1
)=θ-
.(12分)
∴sinA(cosB-cosC)=sinC-sinB
得4sin
| A |
| 2 |
| A |
| 2 |
| B+C |
| 2 |
| B-C |
| 2 |
| B-C |
| 2 |
| B+C |
| 2 |
∵
| B+C |
| 2 |
| π |
| 2 |
| A |
| 2 |
| B+C |
| 2 |
| A |
| 2 |
| B+C |
| 2 |
| A |
| 2 |
| B-C |
| 2 |
∴sin
| A |
| 2 |
| B-C |
| 2 |
| A |
| 2 |
| 1 |
| 2 |
∴A=
| π |
| 2 |
z1
. |
| z2 |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴当0<θ<
| π |
| 2 |
. |
| z2 |
| 3π |
| 2 |
当
| π |
| 2 |
. |
| z2 |
| π |
| 2 |
点评:本题考查三角变换、复数的概念和运算.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
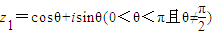 、
、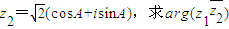 的值.
的值.