题目内容
已知(2x+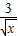 )n展开式中各项系数和为625,则展开式中含x项的系数为( )
)n展开式中各项系数和为625,则展开式中含x项的系数为( )A.216
B.224
C.240
D.250
【答案】分析:利用赋值法求出展开式中各项系数和,列出方程解得n;再利用二项展开式的通项公式求出第r+1项,令x的指数为1求出展开式中含x项的系数.
解答:解:令二项式中的x=1得展开式中各项系数和为5n
∵展开式中各项系数和为625
∴5n=625
∴n=4
∴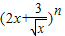 =
=
∴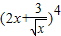 的二项展开式的通项为
的二项展开式的通项为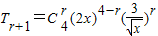 =
=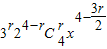
令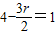 解得r=2
解得r=2
∴展开式中含x项的系数为9×4C42=216
故选A.
点评:本题考查求二项展开式中各项系数和的方法是赋值法;考查二项展开式的通项公式是解决二项展开式的特定项问题的工具.
解答:解:令二项式中的x=1得展开式中各项系数和为5n
∵展开式中各项系数和为625
∴5n=625
∴n=4
∴
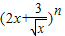 =
=
∴
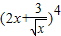 的二项展开式的通项为
的二项展开式的通项为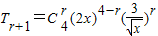 =
=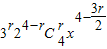
令
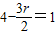 解得r=2
解得r=2∴展开式中含x项的系数为9×4C42=216
故选A.
点评:本题考查求二项展开式中各项系数和的方法是赋值法;考查二项展开式的通项公式是解决二项展开式的特定项问题的工具.

练习册系列答案
相关题目