题目内容
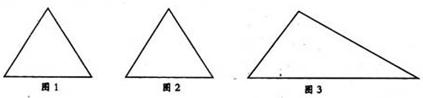
(1)给出两块相同的正三角形纸片(如图1,图2),要求用其中一块剪拼成一个三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设计一种剪拼方法,分别用虚线标示在图1、图2中,并作简要说明;(2)试比较你剪拼的正三棱锥与正三棱柱的体积的大小;
(3)如果给出的是一块任意三角形的纸片(如图3),要求剪栟成一个直三棱柱,使它的全面积与给出的三角形的面积相等.请设计一种剪拼方法,用虚线标示在图3中,并作简要说明.
分析:(1)可以利用正三角形的图形特征,进行分割.
(2)可以直接求解,直接比较大小.
(3)分别连接三角形的内心与各顶点,得三条线段,再以这三条线段的中点为顶点作三角形.以新作的三角形为直棱柱的底面,过新三角形的三个顶点向原三角形三边作垂线,组合就好了.
(2)可以直接求解,直接比较大小.
(3)分别连接三角形的内心与各顶点,得三条线段,再以这三条线段的中点为顶点作三角形.以新作的三角形为直棱柱的底面,过新三角形的三个顶点向原三角形三边作垂线,组合就好了.
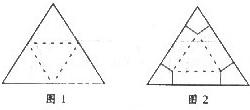
解答:解:(1)如图1,沿正三角形三边中点连线折起,可拼得一个正三棱锥.
如图2,正三角形三个角上剪出三个相同的四边形,其较长的一组邻边边长为三角形边长的
,有一组对角为直角,余下部分按虚线折起,可成一个缺上底的正三棱柱,而剪出的三个相同的四边形恰好拼成这个正三棱锥的上底.
(2)依上面剪拼方法,有V柱>V锥.
推理如下:
设给出正三角形纸片的边长为2,
那么,正三棱锥与正三棱柱的底面都是边长为1的正三角形,其面积为
.
现在计算它们的高:h锥=
=
,h柱=
tan30°=
.V柱-V锥=(h柱-
h锥)•
=(
-
)•
=
>0
所以V柱>V锥.
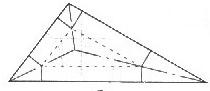
(3)如图,分别连接三角形的内心与各顶点,得三条线段,再以这三条线段的中点为顶点作三角形.以新作的三角形为直棱柱的底面,过新三角形的三个顶点向原三角形三边作垂线,沿六条垂线剪下三个四边形,可心拼成直三棱柱的上底,余下部分按虚线折起,成为一个缺上底的直三棱柱,即可得到直三棱柱.
如图2,正三角形三个角上剪出三个相同的四边形,其较长的一组邻边边长为三角形边长的
| 1 |
| 4 |

(2)依上面剪拼方法,有V柱>V锥.
推理如下:
设给出正三角形纸片的边长为2,
那么,正三棱锥与正三棱柱的底面都是边长为1的正三角形,其面积为
| ||
| 4 |
现在计算它们的高:h锥=
1-(
|
| ||
| 3 |
| 1 |
| 2 |
| ||
| 6 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 6 |
| ||
| 9 |
| ||
| 4 |
3-2
| ||
| 24 |
所以V柱>V锥.
(3)如图,分别连接三角形的内心与各顶点,得三条线段,再以这三条线段的中点为顶点作三角形.以新作的三角形为直棱柱的底面,过新三角形的三个顶点向原三角形三边作垂线,沿六条垂线剪下三个四边形,可心拼成直三棱柱的上底,余下部分按虚线折起,成为一个缺上底的直三棱柱,即可得到直三棱柱.

点评:本题考查学生的空间想象能力,棱锥、棱柱的结构特征,是中档题.

练习册系列答案
相关题目



