题目内容
设数列｛an｝的首项a1＝1，前n项和Sn满足关系式：
3tSn－（2t＋3）Sn－1＝3t（t＞0,n＝2，3，4，…）．
求证：数列｛an｝是等比数列；
答案：
解析：
解析：
（1）由S1＝a1＝1，S2＝a1＋a2＝1＋a2，得3t（1＋a2）－（2t＋3）＝3t， 可得a2＝ 3tSn－1－（2t＋3）Sn－2＝3t，两式相减，得3tan－（2t＋3）an－1＝0． 于是
|
，于是
＝
又3tSn－（2t＋3）Sn－1＝3t，
＝
，n＝3，4…．因此，｛an｝是一个首项为1，公比为
的等比数列．
练习册系列答案
名校课堂系列答案
相关题目
（
｝是等差数列．
（
｝是等差数列．
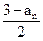（n∈N+）
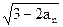，判断数列｛bn｝的单调性，并证明你的结论
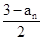（n∈N+）
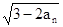，判断数列｛bn｝的单调性，并证明你的结论