题目内容
设等比数列{![]() }的前
}的前![]() 项和
项和![]() ,首项
,首项![]() ,公比
,公比![]() .
.
(1)证明:![]() ;
;
(2)若数列{![]() }满足
}满足![]() ,
,![]() ,求数列{
,求数列{![]() }的通项
}的通项![]() 公式;
公式;
(3)在(2)的结论下,若![]() ,记
,记![]() ,数列{
,数列{![]() }的前n项和为
}的前n项和为![]() ,求证:当
,求证:当![]() 时,
时,![]() .
.
解(1)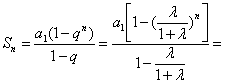
![]()
而![]() ,所以
,所以![]()
(2)![]() ,所以
,所以![]() ,所以
,所以![]()
![]() 是首项为
是首项为![]() ,公差为1的等差数列,所以
,公差为1的等差数列,所以![]() 即
即![]() ………9’
………9’
(3) ![]() 时,
时,![]() ,
, ![]()
![]()
![]()
相减得![]()
![]() ,
,
又因为![]() ,
,![]() 单调递增,
单调递增, ![]() 故当
故当![]() 时,
时, ![]() .
.

练习册系列答案
相关题目
 是首项
是首项 的等比数列,且
的等比数列,且 ,
, ,
, 成等差数列.
成等差数列. ,设
,设 为数列
为数列 的前
的前 项和,若
项和,若 对一切
对一切 恒
恒 的最小值.
的最小值.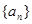 的任意相邻两项为坐标的点
的任意相邻两项为坐标的点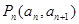 (
(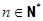 )都在一次函数
)都在一次函数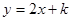 的图象上,数列
的图象上,数列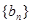 满足
满足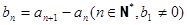 .
.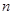 项和分别为
项和分别为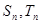 ,且
,且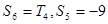 ,求
,求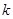 的值.
的值.