题目内容
已知三角形的三边分别为a,b,c,内切圆的半径为r,则三角形的面积S=
(a+b+c)•r,四面体的四个面的面积分别为S1,S2,S3,S4,内切球的半径为R,类比三角形的面积可得四面体的体积为( )
| 1 |
| 2 |
分析:根据平面与空间之间的类比推理,由点类比点或直线,由直线 类比 直线或平面,由内切圆类比内切球,由平面图形面积类比立体图形的体积,结合求三角形的面积的方法类比求四面体的体积即可.
解答: 解:设四面体的内切球的球心为O,
解:设四面体的内切球的球心为O,
则球心O到四个面的距离都是R,
所以四面体的体积等于以O为顶点,
分别以四个面为底面的4个三棱锥体积的和.
类比三角形的面积可得四面体的体积为:V=
R(S1+S2+S3+S4).
故选C.
 解:设四面体的内切球的球心为O,
解:设四面体的内切球的球心为O,则球心O到四个面的距离都是R,
所以四面体的体积等于以O为顶点,
分别以四个面为底面的4个三棱锥体积的和.
类比三角形的面积可得四面体的体积为:V=
| 1 |
| 3 |
故选C.
点评:本题主要考查类比推理.类比推理是指依据两类数学对象的相似性,将已知的一类数学对象的性质类比迁移到另一类数学对象上去.属于基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 ,内切圆的半径为
,内切圆的半径为 ,则三角形的面积为
,则三角形的面积为
 ;四面体的四个面的面积分别为
;四面体的四个面的面积分别为 ,内切球的半径为
,内切球的半径为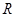 。类比三角形的面积可得四面体的体积为( )。
。类比三角形的面积可得四面体的体积为( )。 B.
B.
 D.
D.