题目内容
已知复数z1=log2(2x+1)+ki,z2=1-xi(其中x,k∈R),记z1z2的实部为f(x),若函数f(x)是关于x的偶函数,(1)求k的值;
(2)求函数y=f(log2x)在x∈(0,a],a>0,a∈R上的最小值;
(3)求证:对任意实数m,函数y=f(x)图象与直线y=
| 1 | 2 |
分析:(1)利用z1z2的实部为f(x),求出f(x),通过函数f(x)是关于x的偶函数,求k的值;
(2)利用(1)求出函数y=f(log2x)的表达式,化简后,通过基本不等式,函数的单调性求出在x∈(0,a],a>0,a∈R上的最小值;
(3)函数y=f(x)图象与直线y=
x+m的图象最多只有一个交点.转化为方程最多只有一个解,图象最多只有一个交点,利用函数的单调性证明即可.
(2)利用(1)求出函数y=f(log2x)的表达式,化简后,通过基本不等式,函数的单调性求出在x∈(0,a],a>0,a∈R上的最小值;
(3)函数y=f(x)图象与直线y=
| 1 |
| 2 |
解答:解:(1)z1z2=(log2(2x+1)+ki)(1-xi);所以f(x)=log2(2x+1)+kx,
因为函数f(x)是关于x的偶函数所以f(-x)=log2(2-x+1)-kx=log2(2x+1)+kx=f(x),所以2kx=-x,所以k=-
(2)由(1)可知f(x)=log2(2x+1)-
x,
所以y=f(log2x)=log2(x+1)-
log2x=log2
=
,
所以x∈(0,a],a>0,a∈R,ymin=
(3)函数y=f(x)图象与直线y=
x+m的图象最多只有一个交点,
就是log2(2x+1)-
x=
x+m最多只有一个解,就是log2(2x+1)=x+m最多只有一个解,
因为函数log2(2x+1)是单调增函数,x+m也是单调增函数,
所以对任意实数m,函数y=f(x)图象与直线y=
x+m的图象最多只有一个交点.
因为函数f(x)是关于x的偶函数所以f(-x)=log2(2-x+1)-kx=log2(2x+1)+kx=f(x),所以2kx=-x,所以k=-
| 1 |
| 2 |
(2)由(1)可知f(x)=log2(2x+1)-
| 1 |
| 2 |
所以y=f(log2x)=log2(x+1)-
| 1 |
| 2 |
| x+1 | ||
|
| log | (
2 |
所以x∈(0,a],a>0,a∈R,ymin=
|
(3)函数y=f(x)图象与直线y=
| 1 |
| 2 |
就是log2(2x+1)-
| 1 |
| 2 |
| 1 |
| 2 |
因为函数log2(2x+1)是单调增函数,x+m也是单调增函数,
所以对任意实数m,函数y=f(x)图象与直线y=
| 1 |
| 2 |
点评:本题是中档题,以复数为依托,考查函数的最值的求法,函数的解与方程的根的知识,考查计算能力,转化思想的应用.

练习册系列答案
相关题目
 的图象最多只有一个交点.
的图象最多只有一个交点.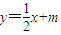 的图象最多只有一个交点.
的图象最多只有一个交点.