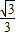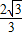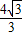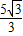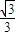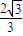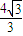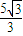题目内容
己知球的直径SC=4,A,B是该球球面上的两点.AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:由题意求出SA=AC=SB=BC=2
,∠SAC=∠SBC=90°,说明球心O与AB的平面与SC垂直,求出OAB的面积,即可求出棱锥S-ABC的体积.
| 2 |
解答: 解:如图:由题意球的直径SC=4,A,B是该球球面上的两点.AB=2,∠ASC=∠BSC=45°,求出SA=AC=SB=BC=2
解:如图:由题意球的直径SC=4,A,B是该球球面上的两点.AB=2,∠ASC=∠BSC=45°,求出SA=AC=SB=BC=2
,
∠SAC=∠SBC=90°,所以平面ABO与SC垂直,则S△ABO=
×22 =
进而可得:VS-ABC=VC-AOB+VS-AOB,
所以棱锥S-ABC的体积为:
×
×4=
.
故选C.
 解:如图:由题意球的直径SC=4,A,B是该球球面上的两点.AB=2,∠ASC=∠BSC=45°,求出SA=AC=SB=BC=2
解:如图:由题意球的直径SC=4,A,B是该球球面上的两点.AB=2,∠ASC=∠BSC=45°,求出SA=AC=SB=BC=2| 2 |
∠SAC=∠SBC=90°,所以平面ABO与SC垂直,则S△ABO=
| ||
| 4 |
| 3 |
进而可得:VS-ABC=VC-AOB+VS-AOB,
所以棱锥S-ABC的体积为:
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
故选C.
点评:本题是基础题,考查球的内接三棱锥的体积,考查空间想象能力,计算能力,球心O与AB的平面与SC垂直是本题的解题关键,常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目