题目内容
已知球面上的四点P，A，B，C，PA，PB，PC的长分别为3、4、5，且这三条线段两两垂直，则这个球的体积为 ．
分析：由题意知球面上的四点P、A、B、C是长方体的一个角，扩展为长方体，长方体的对角线就是外接球的直径，求出直径即求出外接球的体积．
解答：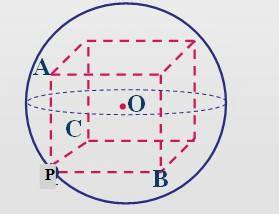
解：球面上的四点P、A、B、C，又PA、PB、PC的长分别为3、4、5，且这三条线段两两垂直，是长方体的一个角，
扩展为长方体，两者的外接球相同，长方体的对角线长为l=
=
，外接球的半径为R=
=
；
∴球的体积为：V=
=
=
．
故答案为：
．
解：球面上的四点P、A、B、C，又PA、PB、PC的长分别为3、4、5，且这三条线段两两垂直，是长方体的一个角，扩展为长方体，两者的外接球相同，长方体的对角线长为l=
| 32+42+52 |
| 50 |
| l |
| 2 |
| ||
| 2 |
∴球的体积为：V=
| 4πR3 |
| 3 |
4π(
| ||||
| 3 |
125
| ||
| 3 |
故答案为：
125
| ||
| 3 |
点评：本题考查了四面体的外接球体积的求法问题，解题时把四面体扩展为长方体，长方体的对角线就是球的直径．
练习册系列答案
走进文言文系列答案
相关题目
已知球面上的四点P、A、B、C，PA、PB、PC的长分别为3、4、5，且这三条线段两两垂直，则这个球的表面积为（ ）
A、20
| ||
B、25
| ||
| C、50π | ||
| D、200π |
,PB=1,PC=2,则A、B两点的球面距离为( )
B.
C.
D.
π B.32
π C.
D.