题目内容
已知边长为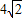 的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行,则AE与平面α间的距离为 .
的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行,则AE与平面α间的距离为 .
【答案】分析:先作出平面α过PF且与AE平行,设H为DF的中点,再作AK⊥PH,则AK⊥面PDF,AK就是AE与平面α的距离,利用等面积可求AE与平面α间的距离.
解答: 解:由题意,延长BA到D,使AD=EF=0.5AB,则四边形AEFD是平行四边形,
解:由题意,延长BA到D,使AD=EF=0.5AB,则四边形AEFD是平行四边形,
∴AE∥DF,则面PDF为α.
∵AE?α,DF?α,
∴AE∥α,
设H为DF的中点,AD=AF=2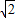 ,
,
∴AH⊥DF,
∵PA⊥面ABC,由三垂线逆定理,DF⊥PH,
∴DF⊥面PAH,
∵DF⊆面PDF
∴面PDF⊥面PAH,
作AK⊥PH,则AK⊥面PDF,AK就是AE与平面α的距离.
∵AH=0.5AD= ,AD=2,
,AD=2,
∴PH= ,AK=
,AK=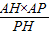 =
=
∴AE与平面α的距离为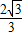
故答案为: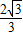
点评:本题考查的重点是线面距离,解题的关键是作出满足题意的平面,将线面距离转化为点面距离求解.
解答:
 解:由题意,延长BA到D,使AD=EF=0.5AB,则四边形AEFD是平行四边形,
解:由题意,延长BA到D,使AD=EF=0.5AB,则四边形AEFD是平行四边形,∴AE∥DF,则面PDF为α.
∵AE?α,DF?α,
∴AE∥α,
设H为DF的中点,AD=AF=2
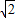 ,
,∴AH⊥DF,
∵PA⊥面ABC,由三垂线逆定理,DF⊥PH,
∴DF⊥面PAH,
∵DF⊆面PDF
∴面PDF⊥面PAH,
作AK⊥PH,则AK⊥面PDF,AK就是AE与平面α的距离.
∵AH=0.5AD=
 ,AD=2,
,AD=2,∴PH=
 ,AK=
,AK=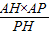 =
=
∴AE与平面α的距离为
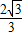
故答案为:
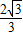
点评:本题考查的重点是线面距离,解题的关键是作出满足题意的平面,将线面距离转化为点面距离求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
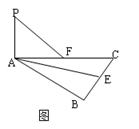
 的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行,则AE与平面α间的距离为________.
的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行,则AE与平面α间的距离为________. 的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行,则AE与平面α间的距离为 .
的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行,则AE与平面α间的距离为 .