题目内容
如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若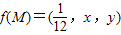 ,且ax+y-108xy≥0恒成立,则正实数a的最小值为 .
,且ax+y-108xy≥0恒成立,则正实数a的最小值为 .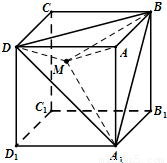
【答案】分析:由已知中M是△A1BD内任一点(不包括边界),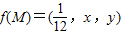 ,结合f(M)=(m,n,p)的定义,我们易得x+y=
,结合f(M)=(m,n,p)的定义,我们易得x+y=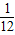 (x>0,y>0),故我们可将ax+y-108xy≥0恒成立,转化为a≥108y-
(x>0,y>0),故我们可将ax+y-108xy≥0恒成立,转化为a≥108y-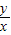 =12-(108x+
=12-(108x+ )恒成立,再由基本不等式求出12-(108x+
)恒成立,再由基本不等式求出12-(108x+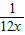 )的最大值,即可得到答案.
)的最大值,即可得到答案.
解答:解:∵M是△A1BD内任一点
∴三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积和等于三锥锥A-A1BD的体积
即f(M)=(m,n,p)中,m+n+p=
当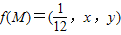 时,可得x+y=
时,可得x+y=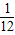 (x>0,y>0)
(x>0,y>0)
若ax+y-108xy≥0恒成立
则a≥108y-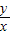 =12-(108x+
=12-(108x+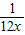 )恒成立,
)恒成立,
∵12-(108x+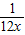 )≤10-6=4
)≤10-6=4
∴正实数a的最小值为4
故答案为:4.
点评:本题考查的知识点是棱锥的体积,基本不等式,其中根据M是△A1BD内任一点,结合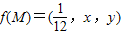 ,得到x+y=
,得到x+y=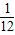 (x>0,y>0),进而将问题转化为函数恒成立问题,是解答本题的关键.
(x>0,y>0),进而将问题转化为函数恒成立问题,是解答本题的关键.
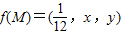 ,结合f(M)=(m,n,p)的定义,我们易得x+y=
,结合f(M)=(m,n,p)的定义,我们易得x+y=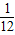 (x>0,y>0),故我们可将ax+y-108xy≥0恒成立,转化为a≥108y-
(x>0,y>0),故我们可将ax+y-108xy≥0恒成立,转化为a≥108y-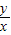 =12-(108x+
=12-(108x+ )恒成立,再由基本不等式求出12-(108x+
)恒成立,再由基本不等式求出12-(108x+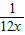 )的最大值,即可得到答案.
)的最大值,即可得到答案.解答:解:∵M是△A1BD内任一点
∴三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积和等于三锥锥A-A1BD的体积
即f(M)=(m,n,p)中,m+n+p=

当
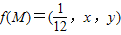 时,可得x+y=
时,可得x+y=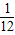 (x>0,y>0)
(x>0,y>0)若ax+y-108xy≥0恒成立
则a≥108y-
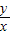 =12-(108x+
=12-(108x+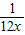 )恒成立,
)恒成立,∵12-(108x+
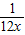 )≤10-6=4
)≤10-6=4∴正实数a的最小值为4
故答案为:4.
点评:本题考查的知识点是棱锥的体积,基本不等式,其中根据M是△A1BD内任一点,结合
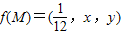 ,得到x+y=
,得到x+y=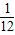 (x>0,y>0),进而将问题转化为函数恒成立问题,是解答本题的关键.
(x>0,y>0),进而将问题转化为函数恒成立问题,是解答本题的关键. 
练习册系列答案
相关题目
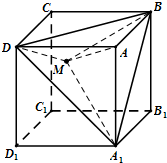 如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若
如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若 (文)如图,在单位正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题:
(文)如图,在单位正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题: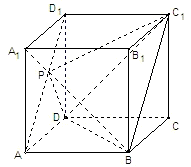 (文)如图,在单位正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题:
(文)如图,在单位正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题: 如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若
如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若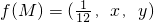 ,且ax+y-108xy≥0恒成立,则正实数a的最小值为________.
,且ax+y-108xy≥0恒成立,则正实数a的最小值为________.