题目内容
下列判断正确的是
- A.函数
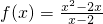 是奇函数
是奇函数 - B.函数
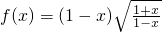 是偶函数
是偶函数 - C.函数
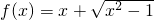 是非奇非偶函数
是非奇非偶函数 - D.函数f(x)=1既是奇函数又是偶函数
C
分析:先考虑函数的定义域是否关于原点对称,再验证f(-x)与f(x)的关系,即可得到结论.
解答:A、函数的定义域为(-∞,2)∪(2,+∞),不关于原点对称,故非奇非偶;
B、函数的定义域为[-1,1),不关于原点对称,故非奇非偶;
C、函数的定义域为(-∞,-1]∪[1,+∞),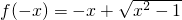 =-
=- ,故非奇非偶;
,故非奇非偶;
D、函数f(x)=1,图象关于y轴对称,是偶函数,但不是奇函数
故选C.
点评:本题考查函数的奇偶性,解题的关键是掌握函数奇偶性的判定步骤,属于中档题.
分析:先考虑函数的定义域是否关于原点对称,再验证f(-x)与f(x)的关系,即可得到结论.
解答:A、函数的定义域为(-∞,2)∪(2,+∞),不关于原点对称,故非奇非偶;
B、函数的定义域为[-1,1),不关于原点对称,故非奇非偶;
C、函数的定义域为(-∞,-1]∪[1,+∞),
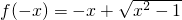 =-
=- ,故非奇非偶;
,故非奇非偶;D、函数f(x)=1,图象关于y轴对称,是偶函数,但不是奇函数
故选C.
点评:本题考查函数的奇偶性,解题的关键是掌握函数奇偶性的判定步骤,属于中档题.

练习册系列答案
相关题目

 为非零实数,代数式
为非零实数,代数式 的值所组成的集合为M,则下列
的值所组成的集合为M,则下列 B.
B.
 C.
C.
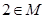 D.
D.

 ,
, ;命题
;命题 ,
, ,则下列判断
,则下列判断 是真命题 B.
是真命题 B.  是假命题 C.
是假命题 C.  是假命题
D.
是假命题
D.  是假命题
是假命题