题目内容
 如图,已知椭圆
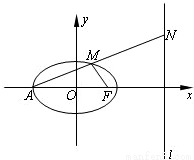
如图,已知椭圆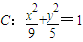 的左顶点、右焦点分别为A、F,右准线为l,N为l上一点,且在x轴上方,AN与椭圆交于点M.
的左顶点、右焦点分别为A、F,右准线为l,N为l上一点,且在x轴上方,AN与椭圆交于点M.(1)若AM=MN,求证:AM⊥MF;
(2)设过A,F,N三点的圆与y轴交于P,Q两点,求PQ的最小值.
【答案】分析:(1)由题意及所给图形,先把点A,F具体,再把点N设出,利用条件解出t,求出kAM•kM若为-1,即可证明;
(2)由题意先设出圆的方程,在利用圆过A,F,N三点,写出圆的方程,由于圆与y轴交于P,Q两点,所以可以令圆的方程中x=0,写出两点坐标利用两点间的距离公式进而求解.
解答:(1)证明:由已知,A(-3,0),F(2,0),设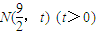 ,
,
则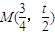 在椭圆
在椭圆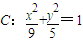 上,得
上,得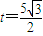 ;
;
∴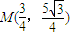 ,∴
,∴ ,
,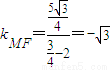 ,
,
∴kAM•kMF=-1,即AM⊥MF;
(2)解:设圆方程为x2+y2+dx+ey+f=0,将A,F,N三点的坐标代入得: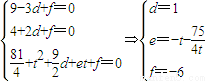 ,
,
∴圆方程为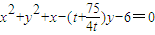 ,令x=0,得:y2+ey-6=0,
,令x=0,得:y2+ey-6=0,
设P(0,y1),Q(0,y2),∴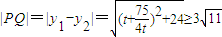 ,∴PQ的最小值为
,∴PQ的最小值为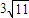 .
.
点评:(1)此问重点考查了利用方程的思想,还考查了利用两条直线的斜率互为负倒数证明直线垂直;
(2)此问重点考查了利用方程的思想进行求解,还考查了利用一元二次函数求解最值及两点间的距离公式.
(2)由题意先设出圆的方程,在利用圆过A,F,N三点,写出圆的方程,由于圆与y轴交于P,Q两点,所以可以令圆的方程中x=0,写出两点坐标利用两点间的距离公式进而求解.
解答:(1)证明:由已知,A(-3,0),F(2,0),设
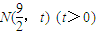 ,
,则
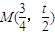 在椭圆
在椭圆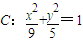 上,得
上,得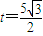 ;
;∴
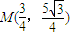 ,∴
,∴ ,
,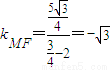 ,
,∴kAM•kMF=-1,即AM⊥MF;
(2)解:设圆方程为x2+y2+dx+ey+f=0,将A,F,N三点的坐标代入得:
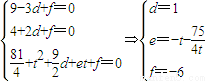 ,
,∴圆方程为
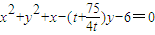 ,令x=0,得:y2+ey-6=0,
,令x=0,得:y2+ey-6=0,设P(0,y1),Q(0,y2),∴
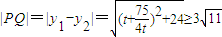 ,∴PQ的最小值为
,∴PQ的最小值为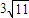 .
.点评:(1)此问重点考查了利用方程的思想,还考查了利用两条直线的斜率互为负倒数证明直线垂直;
(2)此问重点考查了利用方程的思想进行求解,还考查了利用一元二次函数求解最值及两点间的距离公式.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
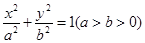 的左顶点为
的左顶点为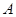 ,左焦点为
,左焦点为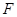 ,上顶点为
,上顶点为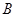 ,若
,若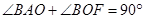 ,则该椭圆的离心率是 .
,则该椭圆的离心率是 .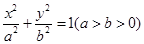 的左顶点为
的左顶点为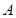 ,左焦点为
,左焦点为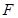 ,上顶点为
,上顶点为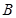 ,若
,若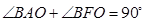 ,则该椭圆的离心率是
.
,则该椭圆的离心率是
.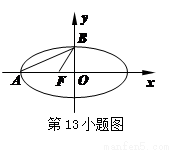
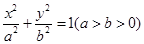 的左顶点为
的左顶点为 ,左焦点为
,左焦点为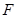 ,上顶点为
,上顶点为 ,若
,若 ,则该椭圆的离心率是
.
,则该椭圆的离心率是
.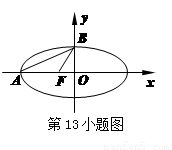
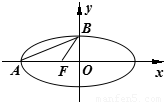 如图,已知椭圆
如图,已知椭圆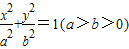 的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则该椭圆的离心率是 .
的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则该椭圆的离心率是 .