题目内容
设有一组圆: ,下列四个命题
,下列四个命题
(1)存在一条定直线与所有的圆均相切;
(2)存在一条定直线与所有的圆均相交;
(3)存在一条定直线与所有的圆均不相交;
(4)所有的圆均不经过原点.
其中真命题的序号是___________.(写出所有的真命题的序号)
【答案】
(2)(4)
【解析】
根据圆的方程可知圆心为(k-1,3k),半径为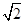 k2,圆心在直线y=3(x+1)上,
k2,圆心在直线y=3(x+1)上,
所以直线y=3(x+1)必与所有的圆相交,②正确;
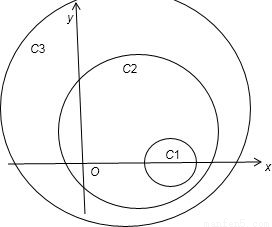
由C1、C2、C3的图象可知①③不正确;
若存在圆过原点(0,0),则有(-k+1)2+9k2=2k4⇒10k2-2k+1=2k4(k∈N*),因为左边为奇数,右边为偶数,
故不存在k使上式成立,即所有圆不过原点,④正确.所以真命题的代号是:②④.故答案为:②④

练习册系列答案
相关题目
 .下列四个命题:
.下列四个命题: .下列四个
.下列四个