题目内容
“m>2”是直线x-my+1=0与圆x2+y2-2x=0相交的
- A.充要条件
- B.充分不必要条件
- C.必要不充分条件
- D.既不充分又不必要条件
B
分析:求出圆x2+y2-2x=0的圆心和半径,由直线x-my+1=0与圆x2+y2-2x=0相交,利用圆心到直线x-my+1=0的距离小于关径就能求出m的范围,然后判断充要条件的关系.
解答:圆x2+y2-2x=0的圆心C(1,O),半径r=1,
∵直线x-my+1=0与圆x2+y2-2x=0相交,
∴圆心C(1,O)到直线x-my+1=0的距离
d=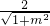 <1=r,
<1=r,
解得m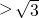 ,或m
,或m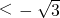 .显然“m>2”时直线x-my+1=0与圆x2+y2-2x=0相交,
.显然“m>2”时直线x-my+1=0与圆x2+y2-2x=0相交,
反之不成立,
所以“m>2”是直线x-my+1=0与圆x2+y2-2x=0相交的充分不必要条件.
故选B.
点评:本题考查直线与圆的位置关系的应用,充要条件的应用.解题时要认真审题,注意点到直线距离公式的合理运用.
分析:求出圆x2+y2-2x=0的圆心和半径,由直线x-my+1=0与圆x2+y2-2x=0相交,利用圆心到直线x-my+1=0的距离小于关径就能求出m的范围,然后判断充要条件的关系.
解答:圆x2+y2-2x=0的圆心C(1,O),半径r=1,
∵直线x-my+1=0与圆x2+y2-2x=0相交,
∴圆心C(1,O)到直线x-my+1=0的距离
d=
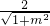 <1=r,
<1=r,解得m
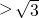 ,或m
,或m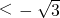 .显然“m>2”时直线x-my+1=0与圆x2+y2-2x=0相交,
.显然“m>2”时直线x-my+1=0与圆x2+y2-2x=0相交,反之不成立,
所以“m>2”是直线x-my+1=0与圆x2+y2-2x=0相交的充分不必要条件.
故选B.
点评:本题考查直线与圆的位置关系的应用,充要条件的应用.解题时要认真审题,注意点到直线距离公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“m>2”是直线x﹣my+1=0与圆x2+y2﹣2x=0相交的( )
|
| A. | 充要条件 | B. | 充分不必要条件 |
|
| C. | 必要不充分条件 | D. | 既不充分又不必要条件 |