题目内容
(2012年高考(重庆理))(本小题满分13分(Ⅰ)小问8分(Ⅱ)小问5分)
设![]() ,其中
,其中![]()
(Ⅰ)求函数![]() 的值域
的值域
(Ⅱ)若![]() 在区间
在区间![]() 上为增函数,求
上为增函数,求 ![]() 的最大值.
的最大值.
【考点定位】本题以三角函数的化简求值为主线,三角函数的性质为考查目的的一道综合题,考查学生分析问题解决问题的能力,由正弦函数的单调性结合条件可列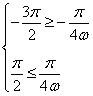 ,从而解得
,从而解得![]() 的取值范围,即可得
的取值范围,即可得![]() 的最在值.
的最在值.
解:(1)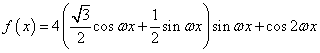
![]()
![]()
因![]() ,所以函数
,所以函数![]() 的值域为
的值域为![]()
(2)因![]() 在每个闭区间
在每个闭区间![]() 上为增函数,故
上为增函数,故![]()
![]() 在每个闭区间
在每个闭区间![]() 上为增函数.
上为增函数.
依题意知![]()
![]() 对某个
对某个![]() 成立,此时必有
成立,此时必有![]() ,于是
,于是
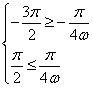 ,解得
,解得![]() ,故
,故![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目