题目内容
已知椭圆 ,满足
,满足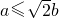 ,若椭圆的离心率为e,则
,若椭圆的离心率为e,则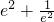 的最小值
的最小值
- A.

- B.

- C.3
- D.4
B
分析:先由a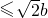 ,及a2=b2+c2,求得椭圆离心率的范围,再利用换元法将函数y=
,及a2=b2+c2,求得椭圆离心率的范围,再利用换元法将函数y=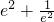 转化为函数y=t+
转化为函数y=t+ (0<t≤
(0<t≤ ),最后利用导数判断此函数的单调性,求出函数的最小值
),最后利用导数判断此函数的单调性,求出函数的最小值
解答:∵a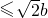 ,∴a2≤2b2,∴a2≤2(a2-c2),即a2≥2c2,∴0<e2≤
,∴a2≤2b2,∴a2≤2(a2-c2),即a2≥2c2,∴0<e2≤
设t=e2,则y=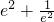 =t+
=t+ (0<t≤
(0<t≤ )
)
∵y′(t)=1- <0,
<0,
∴y=t+ (0<t≤
(0<t≤ )为(0,
)为(0, ]上的减函数
]上的减函数
∴y≥ +
+ =
= ,即
,即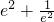 的最小值为
的最小值为
故选B
点评:本题考察了椭圆的几何性质离心率的求法,考察了特殊函数的单调性和最值的求法,注意本题的函数y=t+ (0<t≤
(0<t≤ )不适合用均值定理求最值
)不适合用均值定理求最值
分析:先由a
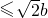 ,及a2=b2+c2,求得椭圆离心率的范围,再利用换元法将函数y=
,及a2=b2+c2,求得椭圆离心率的范围,再利用换元法将函数y=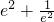 转化为函数y=t+
转化为函数y=t+ (0<t≤
(0<t≤ ),最后利用导数判断此函数的单调性,求出函数的最小值
),最后利用导数判断此函数的单调性,求出函数的最小值解答:∵a
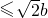 ,∴a2≤2b2,∴a2≤2(a2-c2),即a2≥2c2,∴0<e2≤
,∴a2≤2b2,∴a2≤2(a2-c2),即a2≥2c2,∴0<e2≤
设t=e2,则y=
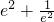 =t+
=t+ (0<t≤
(0<t≤ )
)∵y′(t)=1-
 <0,
<0,∴y=t+
 (0<t≤
(0<t≤ )为(0,
)为(0, ]上的减函数
]上的减函数∴y≥
 +
+ =
= ,即
,即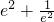 的最小值为
的最小值为
故选B
点评:本题考察了椭圆的几何性质离心率的求法,考察了特殊函数的单调性和最值的求法,注意本题的函数y=t+
 (0<t≤
(0<t≤ )不适合用均值定理求最值
)不适合用均值定理求最值 
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
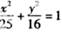 上一点P到其左准线的距离为10,F是该椭圆的左焦点,若点M满足
上一点P到其左准线的距离为10,F是该椭圆的左焦点,若点M满足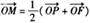 (其中O为坐标原点),则
(其中O为坐标原点),则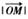 =_________
=_________