题目内容
已知焦点在![]() 轴上的椭圆C1:
轴上的椭圆C1:![]() =1经过A(1,0)点,且离心率为
=1经过A(1,0)点,且离心率为![]() .
.
(I)求椭圆C1的方程;
(Ⅱ)过抛物线C2:![]() (h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与
(h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与![]() 轴平行时,求h的最小值.
轴平行时,求h的最小值.
解:(Ⅰ)由题意可得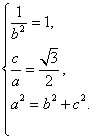 ,……………2分
,……………2分
解得![]() ,
,
所以椭圆![]() 的方程为
的方程为 ![]() .………………4分
.………………4分
(Ⅱ)设![]() ,由
,由 ![]() ,
,
抛物线![]() 在点
在点![]() 处的切线的斜率为
处的切线的斜率为 ![]() ,
,
所以![]() 的方程为
的方程为 ![]() ,……………5分
,……………5分
代入椭圆方程得 ![]() ,
,
化简得 ![]()
又![]() 与椭圆
与椭圆![]() 有两个交点,故
有两个交点,故
![]() ①
①
设![]() ,
,![]() 中点横坐标为
中点横坐标为![]() ,则
,则
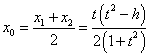 , …………………8分
, …………………8分
设线段![]() 的中点横坐标为
的中点横坐标为![]() ,
,
由已知得![]() 即
即 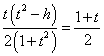 , ②………………10分
, ②………………10分
显然![]() ,
,![]() ③
③
当![]() 时,
时,![]() ,当且仅当
,当且仅当![]() 时取得等号,此时
时取得等号,此时![]() 不符合①式,故舍去;
不符合①式,故舍去;
当![]() 时,
时,![]() ,当且仅当
,当且仅当![]() 时取得等号,此时
时取得等号,此时![]() ,满足①式。
,满足①式。
综上,![]() 的最小值为1.………………12分
的最小值为1.………………12分

练习册系列答案
相关题目
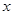 轴上的椭圆
轴上的椭圆 和双曲线
和双曲线 的离心率互为倒数,它们在第一象限交点的坐标为
的离心率互为倒数,它们在第一象限交点的坐标为 ,设直线
,设直线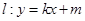 (其中
(其中 为整数).
为整数). 和双曲线
和双曲线 的标准方程;
的标准方程; 与椭圆
与椭圆 ,与双曲线
,与双曲线 ,问是否存在直线
,问是否存在直线 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. 轴上的椭圆的离心率为
轴上的椭圆的离心率为 ,它的长轴长等于圆
,它的长轴长等于圆 的半径,则椭圆的标准方程是( )
的半径,则椭圆的标准方程是( ) B.
B.  C.
C.
 D.
D.
 轴上的椭圆
轴上的椭圆 过点
过点 ,且离心率为
,且离心率为 ,
, 为椭圆
为椭圆 的直线
的直线 与椭圆
与椭圆 ,
, 两点.
两点. 的大小;
的大小;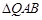 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线 轴上的椭圆
轴上的椭圆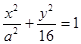 的两个焦点分别为
的两个焦点分别为 , 且
, 且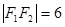 ,弦
,弦 过焦点
过焦点 ,则
,则 的周长为
的周长为 B.
B.  C.
C.  D.
D. 