题目内容
讨论函数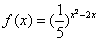
的单调性，并求其值域．
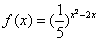的单调性，并求其值域．解：∵函数f(x)的定义域是(-∞，+∞)，
令t=x2-2x，u=(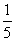
)t，
又∵t=x2-2x=(x-1)2-1在(-∞，1]上是减函数，在[1，+∞)上是增函数，u=(
)t在其定义域内是减函数，
∴函数f(x)在(-∞，1]上为增函数，在[1，+∞)上是减函数．
∵x2-2x=(x-1)2-1≥-1，
又0＜
＜1，
∴函数f(x)的值域是(0，5]．
令t=x2-2x，u=(
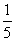)t，又∵t=x2-2x=(x-1)2-1在(-∞，1]上是减函数，在[1，+∞)上是增函数，u=(
)t在其定义域内是减函数， ∴函数f(x)在(-∞，1]上为增函数，在[1，+∞)上是减函数．
∵x2-2x=(x-1)2-1≥-1，
又0＜
＜1， ∴函数f(x)的值域是(0，5]．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
的单调性，并确定它在该区间上的最大值最小值．
为坐标原点，向量
，点是直线
上的一点，且点分有向线段
的比为．（1）记函数
，
，讨论函数
的单调性，并求其值域；（2）若
三点共线，求
的值．
为坐标原点，向量
，
，
，点
满足
.
，
，讨论函数
的单调性，并求其值域；
三点共线，求
的值.
为坐标原点，向量
，
,点
满足
.
，讨论函数
的单调性，并求其值域；
三点共线，求
的值.