题目内容
已知f(x)=| 1 |
| 3 |
| 4x |
| 3x2+3 |
(1)当a=1时,求f(x)在点(3,6)处的切线方程;
(2)求g(x)的值域;
(3)设a>0,若对任意x1∈[0,2],总存在x0∈[0,2],使g(x1)-f(x0)=0,求实数a的取值范围.
分析:(1)将a=1代入求出函数f(x)的解析式,然后求导数,根据k=f'(3)=8,过点(3,6),可得到切线方程.
(2)先求出g(0)=0,然后当x≠0时,对g(x)分子分母同时除以x构成g(x)=
•
,再由基本不等式可求出g(x)的范围,进而确定函数g(x)的值域.
(3)先可以确定函数g(x)的值域是函数f(x)的值域的子集,转化为求函数f(x)在[0,2]上的值域的问题.对函数f(x)进行求导,令导函数等于0求出x的值,再根据导数判断函数在[0,2]上的单调性,可表示出函数在[0,2]上的值域,再由函数g(x)的值域是函数f(x)的值域的子集可得到答案.
(2)先求出g(0)=0,然后当x≠0时,对g(x)分子分母同时除以x构成g(x)=
| 4 |
| 3 |
| 1 | ||
x+
|
(3)先可以确定函数g(x)的值域是函数f(x)的值域的子集,转化为求函数f(x)在[0,2]上的值域的问题.对函数f(x)进行求导,令导函数等于0求出x的值,再根据导数判断函数在[0,2]上的单调性,可表示出函数在[0,2]上的值域,再由函数g(x)的值域是函数f(x)的值域的子集可得到答案.
解答:解:(1)当a=1时,f(x)=
x3-x,
∴f'(x)=x2-1,f'(3)=8
∴切线方程为y-6=8(x-3),即8x-y-18=0
(2)g(x)=
x∈[0,2]
x=0时g(x)=0,0<x≤2时,g(x)=
•
≤
•
=
•
=
,
且g(x)>0,当且仅当x=1时上式取等号即0<g(x)≤
,
综上,g(x)的值域为[0,
].
(3)设函数f(x)在[0,2]上的值域是A,若对任意x1∈[0,2].
总存在x0∈[0,2],使g(x1)-f(x0)=0,∴[0,
]⊆A
由f(x)=
ax3-a2x得f′(x)=ax2-a2=a(x+
)(x-
),x∈(0,2)
令f'(x)=0,得x=
或x=-
(舍去)
(i)0<
<2时,x,f'(x),f(x)的变化如下表:
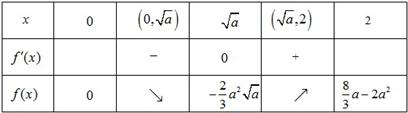
∴f(0)=0, f(
)<0.∴f(2)=
a-2a2≥
,解得
≤a≤1
(ii)当
≥2时,f'(x)<0∴函数f(x)在(0,2)上单调递减.
∵f(0)=0,f(2)=
a-2a2<0,∴当x∈[0,2]时,不满足[0,
]⊆A
综上可知,实数a的取值范围是[
,1].
| 1 |
| 3 |
∴f'(x)=x2-1,f'(3)=8
∴切线方程为y-6=8(x-3),即8x-y-18=0
(2)g(x)=
| 4x |
| 3x2+3 |
x=0时g(x)=0,0<x≤2时,g(x)=
| 4 |
| 3 |
| 1 | ||
x+
|
| 4 |
| 3 |
| 1 | ||||
2
|
| 4 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
且g(x)>0,当且仅当x=1时上式取等号即0<g(x)≤
| 2 |
| 3 |
综上,g(x)的值域为[0,
| 2 |
| 3 |
(3)设函数f(x)在[0,2]上的值域是A,若对任意x1∈[0,2].
总存在x0∈[0,2],使g(x1)-f(x0)=0,∴[0,
| 2 |
| 3 |
由f(x)=
| 1 |
| 3 |
| a |
| a |
令f'(x)=0,得x=
| a |
| a |
(i)0<
| a |

∴f(0)=0, f(
| a |
| 8 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
(ii)当
| a |
∵f(0)=0,f(2)=
| 8 |
| 3 |
| 2 |
| 3 |
综上可知,实数a的取值范围是[
| 1 |
| 3 |
点评:本题主要考查导数的几何意义、函数的单调性与其导函数的正负之间的关系和函数在闭区间上的最值.导数是高考必考题,要准备充分.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
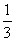 (m∈R,e=2.718 28…是自然对数的底数).
(m∈R,e=2.718 28…是自然对数的底数).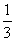 (m∈R,e=2.718 28…是自然对数的底数).
(m∈R,e=2.718 28…是自然对数的底数).