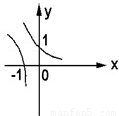
题目内容
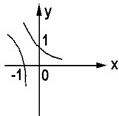 在同一坐标系内作出的两个函数图象如图所示,则这两个函数为( )
在同一坐标系内作出的两个函数图象如图所示,则这两个函数为( )分析:先由指数函数的图象确定函数底数的取值范围,再由此推断对数复合函数的图象性质,并与已知图象比较,若矛盾则排除
解答:解:对于选项A,由图可知y=ax为减函数,故0<a<1,此时y=loga(-x)应为(-∞,0)上的增函数,与图象矛盾,排除A
对于选项B,由图可知y=ax为减函数,故0<a<1,此时y=loga(
)应为(0,+∞)上的增函数,与图象矛盾,排除B
对于选项C,由图可知y=a-x为减函数,故a>1,此时y=loga(
)应为(0,+∞)上的减函数,与图象矛盾,排除C
故选D
对于选项B,由图可知y=ax为减函数,故0<a<1,此时y=loga(
| 1 |
| x |
对于选项C,由图可知y=a-x为减函数,故a>1,此时y=loga(
| 1 |
| x |
故选D
点评:本题考查了指数函数的图象和性质,对数函数的图象和性质,排除法解选择题

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
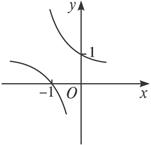
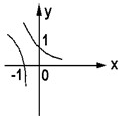 在同一坐标系内作出的两个函数图象如图所示,则这两个函数为
在同一坐标系内作出的两个函数图象如图所示,则这两个函数为