题目内容
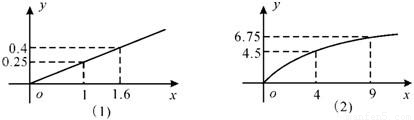
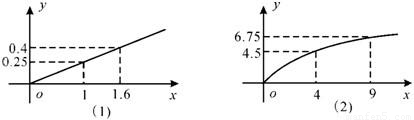
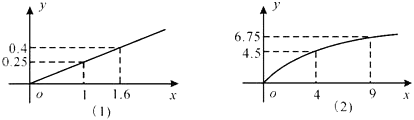
某化工企业生产甲、乙两种产品.根据市场调查与预测,甲产品的利润与投资成正比,其关系如图(1)所示;乙产品的利润与投资的算术平方根成正比,其关系如图(2)所示.(Ⅰ)分别将甲、乙两种产品的利润表示为投资的函数关系式;
(Ⅱ)设该企业准备投资100万元资金,并全部投入甲、乙两种产品的生产.怎样分配这100万元资金,才能使企业获得最大利润,其最大利润为多少万元?(精确到1万元)
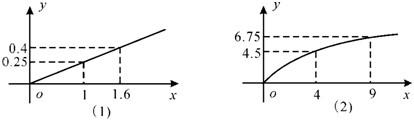
分析:(Ⅰ)先设投资为x万元,写出甲产品的利润、乙产品的利润,根据图形可得甲、乙两种产品的利润表示为投资的函数关系式;(Ⅱ)设甲产品投入x万元,则乙产品投入为100-x万元,得出企业利润的函数表达式,再利用换元法将原函数的最值问题转化成二次函数的最大值问题解决即可得当甲产品投入多少万元,企业获得最大利润.
解答:解:(Ⅰ)设投资为x万元,甲产品的利润为f(x)万元,
乙产品的利润为g(x)万元
由题设f(x)=mx,g(x)=n
(mn≠0)(2分)
由图(1)可知f(1)=0.25=
∴m=
,
由图(2)可知g(4)=4.5=
,∴n=
(4分)
∴f(x)=
x(x≥0),g(x)=
(x≥0)(6分)
(Ⅱ)设甲产品投入x万元,则乙产品投入为100-x万元,设企业利润为y万元
则y=f(x)+g(100-x)=
x+
(0≤x≤100)(8分)
设
=t,则0≤t≤10
y=
+
t=-
t2+
t+25=-
(t-
)2+
(0≤t≤10)
∴t=
时,ymax=
≈30,此时x=79.75(10分)
∴当甲产品投入79.75万元,则乙产品投入为20.25万元时,企业获得的最大利润为30万元.(12分)
乙产品的利润为g(x)万元
由题设f(x)=mx,g(x)=n
| x |
由图(1)可知f(1)=0.25=
| 1 |
| 4 |
| 1 |
| 4 |
由图(2)可知g(4)=4.5=
| 9 |
| 2 |
| 9 |
| 4 |
∴f(x)=
| 1 |
| 4 |
| 9 |
| 4 |
| x |
(Ⅱ)设甲产品投入x万元,则乙产品投入为100-x万元,设企业利润为y万元
则y=f(x)+g(100-x)=
| 1 |
| 4 |
| 9 |
| 4 |
| 100-x |
设
| 100-x |
y=
| 100-t2 |
| 4 |
| 9 |
| 4 |
| 1 |
| 4 |
| 9 |
| 4 |
| 1 |
| 4 |
| 9 |
| 2 |
| 481 |
| 16 |
∴t=
| 9 |
| 2 |
| 481 |
| 16 |
∴当甲产品投入79.75万元,则乙产品投入为20.25万元时,企业获得的最大利润为30万元.(12分)
点评:解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.构造二次函数模型,函数解析式求解是关键,然后利用配方法、数形结合法等方法求解二次函数最值.

练习册系列答案
相关题目