题目内容
(本小题满分14分)
某市拟在长为 的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数
的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数 ,
, 的图象,且图象的最高点为
的图象,且图象的最高点为 ;赛道的后一部分为折线段MNP。为保证参赛运动员的安全,限定
;赛道的后一部分为折线段MNP。为保证参赛运动员的安全,限定 .
.

(1)求 的值和M、P两点间的距离;
的值和M、P两点间的距离;
(2)应如何设计,才能使折线段赛道MNP最长。
某市拟在长为
 的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数
的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数 ,
, 的图象,且图象的最高点为
的图象,且图象的最高点为 ;赛道的后一部分为折线段MNP。为保证参赛运动员的安全,限定
;赛道的后一部分为折线段MNP。为保证参赛运动员的安全,限定 .
.
(1)求
 的值和M、P两点间的距离;
的值和M、P两点间的距离;(2)应如何设计,才能使折线段赛道MNP最长。
解:(1)依题意,有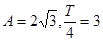 ,又
,又
所以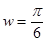 ,所以
,所以 ;
;
当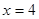 时,
时,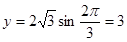 ,所以
,所以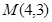
又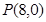 ,所以
,所以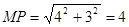
(2) 在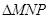 中,
中,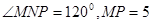
设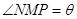 ,则
,则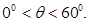
由正弦定理得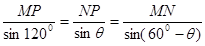
所以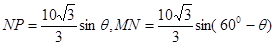
故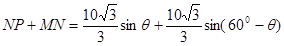
=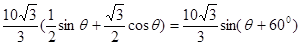
因为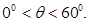 ,当
,当 时,折线段赛道MNP最长。
时,折线段赛道MNP最长。
即将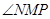 设计为
设计为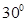 时,折线段赛道 MNP最长。
时,折线段赛道 MNP最长。
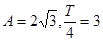 ,又
,又
所以
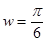 ,所以
,所以 ;
;当
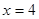 时,
时,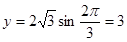 ,所以
,所以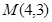
又
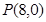 ,所以
,所以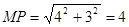
(2) 在
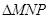 中,
中,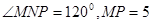
设
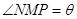 ,则
,则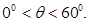
由正弦定理得
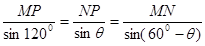
所以
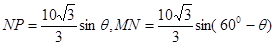
故
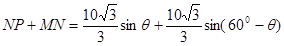
=
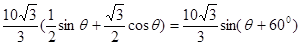
因为
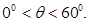 ,当
,当 时,折线段赛道MNP最长。
时,折线段赛道MNP最长。即将
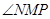 设计为
设计为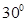 时,折线段赛道 MNP最长。
时,折线段赛道 MNP最长。略

练习册系列答案
相关题目
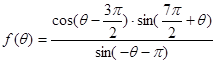
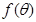 ;
;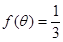 ,求
,求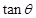 的值;
的值;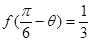 ,求
,求 的值.
的值. 对任意的
对任意的 都有
都有 成立,则
成立,则 的最小值为
的最小值为
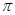 cm,中心角为120o的弧长为
cm,中心角为120o的弧长为 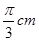



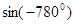 的值是( )
的值是( )
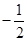

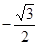
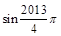 等于( )
等于( )
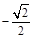
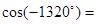 ( )
( )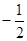
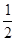
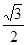
 ,半径为
,半径为 ,则扇形的面积为________.
,则扇形的面积为________.