题目内容
设f(x)是定 义在R上的一个给定的函数,函数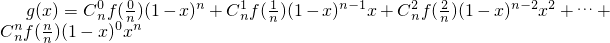 (x≠0,1)
(x≠0,1)
(1)当f(x)=1时,求g(x);
(2)当 f(x)=x时,求g(x).
解:(1)当f(x)=1时,g(x)= (1-x)n+
(1-x)n+ (1-x)n-1•x+…+
(1-x)n-1•x+…+ (1-x)0•xn
(1-x)0•xn
=[(1-x)+x]n
=1;
(2)∵f(x)=x时,g(x)的通项中的二项式系数为: •
•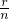 =
=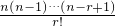 •
•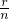 =
=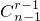 ,
,
∴g(x)=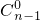 •(1-x)n-1•x+
•(1-x)n-1•x+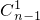 •(1-x)n-2•x•x+
•(1-x)n-2•x•x+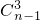 •(1-x)n-3•x2•x+…+
•(1-x)n-3•x2•x+…+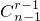 •(1-x)(n-1)-(r-1)•xr-1•x+…+
•(1-x)(n-1)-(r-1)•xr-1•x+…+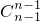 •(1-x)0•xn-1•x
•(1-x)0•xn-1•x
=x[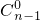 •(1-x)n-1+
•(1-x)n-1+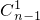 •(1-x)n-2•x+
•(1-x)n-2•x+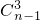 •(1-x)n-3•x2+…+
•(1-x)n-3•x2+…+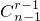 •(1-x)(n-1)-(r-1)•xr-1+…+
•(1-x)(n-1)-(r-1)•xr-1+…+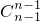 •(1-x)0•xn-1]
•(1-x)0•xn-1]
=x[(1-x)+x]n-1
=x.
分析:(1)当f(x)=1时,g(x)= (1-x)n+
(1-x)n+ (1-x)n-1•x+…+
(1-x)n-1•x+…+ (1-x)0•xn=[(1-x)+x]n,从而可得答案;
(1-x)0•xn=[(1-x)+x]n,从而可得答案;
(2)当 f(x)=x时,g(x)的通项中的二项式系数可化为: •
•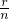 =
=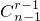 ,逆用二项式定理即可得到g(x)的表达式.
,逆用二项式定理即可得到g(x)的表达式.
点评:本题考察二项式定理的应用,逆用二项式定理是解决问题的关键,求得 •
•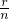 =
=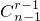 是基础,考察学生观察问题、分析问题、解决问题的综合素质,属于难题.
是基础,考察学生观察问题、分析问题、解决问题的综合素质,属于难题.
 (1-x)n+
(1-x)n+ (1-x)n-1•x+…+
(1-x)n-1•x+…+ (1-x)0•xn
(1-x)0•xn=[(1-x)+x]n
=1;
(2)∵f(x)=x时,g(x)的通项中的二项式系数为:
 •
•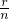 =
=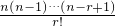 •
•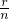 =
=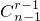 ,
,∴g(x)=
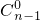 •(1-x)n-1•x+
•(1-x)n-1•x+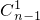 •(1-x)n-2•x•x+
•(1-x)n-2•x•x+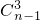 •(1-x)n-3•x2•x+…+
•(1-x)n-3•x2•x+…+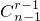 •(1-x)(n-1)-(r-1)•xr-1•x+…+
•(1-x)(n-1)-(r-1)•xr-1•x+…+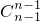 •(1-x)0•xn-1•x
•(1-x)0•xn-1•x=x[
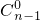 •(1-x)n-1+
•(1-x)n-1+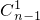 •(1-x)n-2•x+
•(1-x)n-2•x+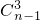 •(1-x)n-3•x2+…+
•(1-x)n-3•x2+…+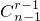 •(1-x)(n-1)-(r-1)•xr-1+…+
•(1-x)(n-1)-(r-1)•xr-1+…+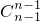 •(1-x)0•xn-1]
•(1-x)0•xn-1]=x[(1-x)+x]n-1
=x.
分析:(1)当f(x)=1时,g(x)=
 (1-x)n+
(1-x)n+ (1-x)n-1•x+…+
(1-x)n-1•x+…+ (1-x)0•xn=[(1-x)+x]n,从而可得答案;
(1-x)0•xn=[(1-x)+x]n,从而可得答案;(2)当 f(x)=x时,g(x)的通项中的二项式系数可化为:
 •
•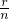 =
=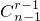 ,逆用二项式定理即可得到g(x)的表达式.
,逆用二项式定理即可得到g(x)的表达式.点评:本题考察二项式定理的应用,逆用二项式定理是解决问题的关键,求得
 •
•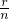 =
=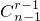 是基础,考察学生观察问题、分析问题、解决问题的综合素质,属于难题.
是基础,考察学生观察问题、分析问题、解决问题的综合素质,属于难题. 
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目