题目内容
已知平面区域U={(x,y)|x+y≤6,x≥0,y≥0},A={(x,y)|x≤4,y≥0,x-2y≥0},若向区域U内随机投一点P,则点P落入区域A的概率为分析:本题考查的知识点是几何概型的意义,关键是要找出A={(x,y)|x≤4,y≥0,x-2y≥0}对应面积的大小,然后将其代入几何概型的计算公式进行求解.在解题过程中,注意三角形面积的应用.
解答: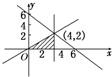 解:依题意可在平面直角坐标系中作出集合U与A所表示的平面区域(如图),
解:依题意可在平面直角坐标系中作出集合U与A所表示的平面区域(如图),
由图可知SU=18,SA=4,
则点P落入区域A的概率为
=
.
故答案为:
.
 解:依题意可在平面直角坐标系中作出集合U与A所表示的平面区域(如图),
解:依题意可在平面直角坐标系中作出集合U与A所表示的平面区域(如图),由图可知SU=18,SA=4,
则点P落入区域A的概率为
| SA |
| SU |
| 2 |
| 9 |
故答案为:
| 2 |
| 9 |
点评:本题考查的知识点是几何概型的意义,关键是要找出A={(x,y)|x≤4,y≥0,x-2y≥0}对应面积的大小,并将其和长方形面积一齐代入几何概型计算公式进行求解.几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目