题目内容
如图,F1,F2分别是椭圆C: +
+ =1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°
=1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°

(1)求椭圆C的离心率;
(2)已知△AF1B的面积为40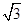 ,求a,b的值
,求a,b的值
【答案】
(1)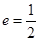 ;(2)
;(2)
【解析】
试题分析:(1)要掌握椭圆的几何性质以及图形中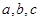 对应的线段,上图中,
对应的线段,上图中,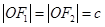 ,
,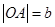 ,
, (2)可用代数法,以
(2)可用代数法,以 为参数,写出直线
为参数,写出直线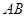 方程,与椭圆方程联立求出
方程,与椭圆方程联立求出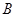 点坐标,从而求出
点坐标,从而求出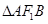 的面积,再利用面积为
的面积,再利用面积为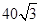 ,求出
,求出 ,即求出
,即求出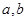 ;当然也可几何方法,由于
;当然也可几何方法,由于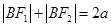 ,在
,在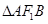 中利用余弦定理,可把
中利用余弦定理,可把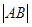 用
用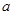 表示出来,再利用
表示出来,再利用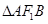 面积为
面积为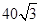 ,可求出
,可求出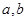
试题解析:(1)由题意可知,△AF1F2为等边三角形,a=2c,所以e=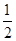 3
3
(2)( 方法一)a2=4c2,b2=3c2
直线AB的方程可为y=-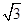 (x-c)
(x-c)
将其代入椭圆方程3x2+4y2=12c2, 5
得B 7
7
所以|AB|=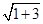 ·
· =
=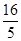 c 9
c 9
由S△AF1B=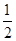 |AF1|·|AB|sin∠F1AB
10
|AF1|·|AB|sin∠F1AB
10
=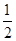 a·
a·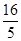 c·
c·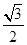 =
=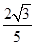 a2=40
a2=40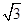 ,
,
解得a=10,b=5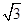 12
12
(方法二)设|AB|=t
因为|AF2|=a,所以|BF2|=t-a
由椭圆定义|BF1|+|BF2|=2a可知,|BF1|=3a-t
再由余弦定理(3a-t)2=a2+t2-2atcos60°可得,
t=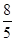 a
a
由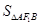 =
=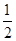 a·
a·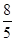 a·
a·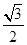 =
=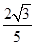 a2=40
a2=40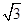 知,a=10,b=5
知,a=10,b=5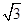
考点:(1)椭圆的离心率;(2)椭圆的定义和三角形的面积、余弦定理

练习册系列答案
相关题目
 如图,F1,F2分别为椭圆
如图,F1,F2分别为椭圆 如图,F1、F2分别为椭圆
如图,F1、F2分别为椭圆 如图,F1,F2分别为双曲线
如图,F1,F2分别为双曲线 如图,F1、F2分别为椭圆
如图,F1、F2分别为椭圆 的左、右焦点,点P在椭圆上,△POF2是面积
的左、右焦点,点P在椭圆上,△POF2是面积 的正三角形,则
的正三角形,则 的值是
的值是