题目内容
已知n为等差数列-4,-2,0,…中的第8项,则二项式(x2+
)n展开式中常数项是( )
| 2 | ||
|
| A、第7项 | B、第8项 |
| C、第9项 | D、第10项 |
分析:根据等差数列的前几项可以看出数列的首项和公差,写出等差数列的通项公式,得到第八项的值,即知道了二项式的指数是10,写出二项式的通项,使它的x的指数为0,得到r的值,得到结果.
解答:解:∵由前几项可得通项为
am=2m-6,
∴a8=2×8-6=10,
∴Tr+1=C10rx20-2r•2rx-
=2rC10rx20-
r,
令20-
r=0,
得r=8.
∴故为8+1=9项,
故选C.
am=2m-6,
∴a8=2×8-6=10,
∴Tr+1=C10rx20-2r•2rx-
| r |
| 2 |
| 5 |
| 2 |
令20-
| 5 |
| 2 |
得r=8.
∴故为8+1=9项,
故选C.
点评:本题看出等差数列的通项公式,二项式定理的特征项,是一个综合题,解题的关键是得到二项式中指数的值,写出通项,得到常数项,这是二项式中常考到的知识点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
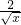 )n展开式中常数项是
)n展开式中常数项是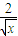 )n展开式中常数项是( )
)n展开式中常数项是( )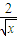 )n展开式中常数项是( )
)n展开式中常数项是( )